C# || Word Search – How To Search A Grid Matrix For A Target Word Using C#
The following is a module with functions which demonstrates how to search a grid matrix for a target word using C#.
1. Word Search – Problem Statement
Given an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example 1:
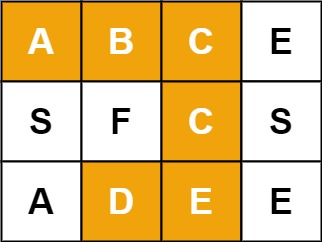
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true
Example 2:
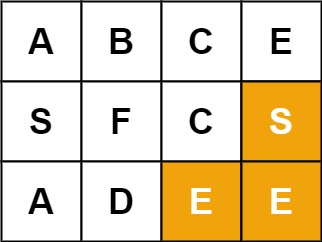
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true
Example 3:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false
2. Word Search – Solution
The following is a solution which demonstrates how to search a grid matrix for a target word. This solution uses Depth First Search.
Depth First Search (DFS) is an algorithm for searching tree or graph data structures. It starts at the root node and explores as far as possible along each branch before backtracking.
In this problem we start at the root node and search all the possibilities at each array index until a match is found. We create a ‘visited’ array to keep track of the indexes already seen.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 11, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Determines if a word can be constructed from letters in a grid // ============================================================================ public class Solution { public bool Exist(char[][] board, string word) { // Create a 2D bool 'visited' node matrix to keep track of the // items we've already seen var rowsVisited = new bool[board.Length][]; for (int rowIndex = 0; rowIndex < board.Length; ++rowIndex) { rowsVisited[rowIndex] = new bool[board[rowIndex].Length]; } // Start at the root node and explore as far as possible along each branch for (int rowIndex = 0; rowIndex < board.Length; ++rowIndex) { for (int colIndex = 0; colIndex < board[rowIndex].Length; ++colIndex) { if (DFS(board, rowIndex, colIndex, 0, word, rowsVisited)) { return true; } } } return false; } private bool DFS(char[][] board, int row, int col, int searchIndex, string word, bool[][] rowsVisited) { // This is the success case if (searchIndex >= word.Length) { return true; } // Make sure the search parameters are in bounds if (row < 0 || row >= board.Length || col < 0 || col >= board[row].Length) { return false; } if (rowsVisited[row][col]) { return false; } if (board[row][col] != word[searchIndex]) { return false; } // Mark that this row has been visited rowsVisited[row][col] = true; var searchResult = // Search left DFS(board, row, col - 1, searchIndex + 1, word, rowsVisited) || // Search right DFS(board, row, col + 1, searchIndex + 1, word, rowsVisited) || // Search top DFS(board, row - 1, col, searchIndex + 1, word, rowsVisited) || // Search bottom DFS(board, row + 1, col, searchIndex + 1, word, rowsVisited); // Unmark that this row has been visited rowsVisited[row][col] = false; return searchResult; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
true
true
false
Hi, I'm a software engineer. I write articles about programming and design in my spare time.
Leave a Reply