November 2021 – My Programming Notes

Monthly Archives: November 2021

C# || String To Integer (atoi) – How To Convert String To Signed Integer Using C#

November 30, 2021 admin 1 Comment

The following is a module with functions which demonstrates how to convert a string to 32-bit signed integer using C#.

1. My Atoi – Problem Statement

Implement the myAtoi(string s) function, which converts a string to a 32-bit signed integer (similar to C/C++’s atoi function).

The algorithm for myAtoi(string s) is as follows:

Read in and ignore any leading whitespace.
Check if the next character (if not already at the end of the string) is ‘-‘ or ‘+’. Read this character in if it is either. This determines if the final result is negative or positive respectively. Assume the result is positive if neither is present.
Read in next the characters until the next non-digit character or the end of the input is reached. The rest of the string is ignored.
Convert these digits into an integer (i.e. “123” -> 123, “0032” -> 32). If no digits were read, then the integer is 0. Change the sign as necessary (from step 2).
If the integer is out of the 32-bit signed integer range [-2³¹, 2³¹ – 1], then clamp the integer so that it remains in the range. Specifically, integers less than -2³¹ should be clamped to -2³¹, and integers greater than 2³¹ – 1 should be clamped to 2³¹ – 1.
Return the integer as the final result.

Note:

Only the space character ‘ ‘ is considered a whitespace character.
Do not ignore any characters other than the leading whitespace or the rest of the string after the digits.

Example 1:

Input: s = "42" Output: 42 Explanation: The underlined characters are what is read in, the caret is the current reader position. Step 1: "42" (no characters read because there is no leading whitespace) ^ Step 2: "42" (no characters read because there is neither a '-' nor '+') ^ Step 3: "42" ("42" is read in) ^ The parsed integer is 42. Since 42 is in the range [-2³¹, 2³¹ - 1], the final result is 42.

Example 2:

Input: s = " -42" Output: -42 Explanation: Step 1: " -42" (leading whitespace is read and ignored) ^ Step 2: " -42" ('-' is read, so the result should be negative) ^ Step 3: " -42" ("42" is read in) ^ The parsed integer is -42. Since -42 is in the range [-2³¹, 2³¹ - 1], the final result is -42.

Example 3:

Input: s = "4193 with words" Output: 4193 Explanation: Step 1: "4193 with words" (no characters read because there is no leading whitespace) ^ Step 2: "4193 with words" (no characters read because there is neither a '-' nor '+') ^ Step 3: "4193 with words" ("4193" is read in; reading stops because the next character is a non-digit) ^ The parsed integer is 4193. Since 4193 is in the range [-2³¹, 2³¹ - 1], the final result is 4193.

Example 4:

Input: s = "words and 987" Output: 0 Explanation: Step 1: "words and 987" (no characters read because there is no leading whitespace) ^ Step 2: "words and 987" (no characters read because there is neither a '-' nor '+') ^ Step 3: "words and 987" (reading stops immediately because there is a non-digit 'w') ^ The parsed integer is 0 because no digits were read. Since 0 is in the range [-2³¹, 2³¹ - 1], the final result is 0.

Example 5:

Input: s = "-91283472332" Output: -2147483648 Explanation: Step 1: "-91283472332" (no characters read because there is no leading whitespace) ^ Step 2: "-91283472332" ('-' is read, so the result should be negative) ^ Step 3: "-91283472332" ("91283472332" is read in) ^ The parsed integer is -91283472332. Since -91283472332 is less than the lower bound of the range [-2³¹, 2³¹ - 1], the final result is clamped to -2³¹ = -2147483648.

2. My Atoi – Solution

The following is a solution which demonstrates how to convert a string to 32-bit signed integer.





		
		
			2. My Atoi - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to convert string to integer
// ============================================================================
public class Solution {
    public int MyAtoi(string s) {
        // 1. Advance leading whitespace
        var index = 0;
        while (index < s.Length && char.IsWhiteSpace(s[index])) {
            ++index;
        }

        // 2. Determine if number is positive or negative
        var sign = 1;
        if (index < s.Length && (s[index] == '-' || s[index] == '+')) {
            if (s[index] == '-') {
                sign = -1;
            }
            ++index;
        }

        // 3. Convert char digits to numeric value
        var result = 0;
        while (index < s.Length && char.IsDigit(s[index])) {
            var digit = CharToInt(s[index]);
            // Check for overflow
            if (result > (int.MaxValue - digit) / 10) {
                return sign == -1 ? int.MinValue : int.MaxValue;
            }
            result = (result * 10) + digit;
            ++index;
        }
        return result * sign;
    }

    private static int CharToInt(char ch) {
        return ch - '0';
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to convert string to integer
// ============================================================================
public class Solution {
    public int MyAtoi(string s) {
        // 1. Advance leading whitespace
        var index = 0;
        while (index < s.Length && char.IsWhiteSpace(s[index])) {
            ++index;
        }
 
        // 2. Determine if number is positive or negative
        var sign = 1;
        if (index < s.Length && (s[index] == '-' || s[index] == '+')) {
            if (s[index] == '-') {
                sign = -1;
            }
            ++index;
        }
 
        // 3. Convert char digits to numeric value
        var result = 0;
        while (index < s.Length && char.IsDigit(s[index])) {
            var digit = CharToInt(s[index]);
            // Check for overflow
            if (result > (int.MaxValue - digit) / 10) {
                return sign == -1 ? int.MinValue : int.MaxValue;
            }
            result = (result * 10) + digit;
            ++index;
        }
        return result * sign;
    }
 
    private static int CharToInt(char ch) {
        return ch - '0';
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

42 -42 4193 0 -2147483648

C# || Maximal Rectangle – How To Find Largest Rectangle Area Using C#

November 30, 2021 admin No comments

The following is a module with functions which demonstrates how to find the largest rectangle area containing only 1’s using C#.

1. Maximal Rectangle – Problem Statement

Given a rows x cols binary matrix filled with 0‘s and 1‘s, find the largest rectangle containing only 1‘s and return its area.

Example 1:

Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] Output: 6 Explanation: The maximal rectangle is shown in the above picture.

Example 2:

Input: matrix = [] Output: 0

Example 3:

Input: matrix = [["0"]] Output: 0

Example 4:

Input: matrix = [["1"]] Output: 1

Example 5:

Input: matrix = [["0","0"]] Output: 0

2. Maximal Rectangle – Solution

The following is a solution which demonstrates how to find the largest rectangle area containing only 1’s.

This solution uses the monotonic stack approach.





		
		
			2. Maximal Rectangle - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the largest rectangle area
// ============================================================================
public class Solution {
    public int MaximalRectangle(char[][] matrix) {
        if (matrix.Length == 0) {
            return 0;
        }

        var result = 0;
        var histogram = new int[matrix[0].Length + 1];
        for (int row = 0; row < matrix.Length; ++row) {
            var stack = new Stack<int>();
            for (int col = 0; col <= matrix[row].Length; ++col) {
                // Set value
                if (col < matrix[row].Length) {
                    if (matrix[row][col] == '1') {
                        histogram[col] += 1;
                    } else {
                        histogram[col] = 0;
                    }
                }

                // Compute area
                while (stack.Count > 0 && histogram[stack.Peek()] >= histogram[col]) {
                    var area = histogram[stack.Pop()] * (stack.Count == 0 ? col : (col - stack.Peek() - 1));
                    result = Math.Max(result, area);
                }
                stack.Push(col);
            }
        }
        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the largest rectangle area
// ============================================================================
public class Solution {
    public int MaximalRectangle(char[][] matrix) {
        if (matrix.Length == 0) {
            return 0;
        }
 
        var result = 0;
        var histogram = new int[matrix[0].Length + 1];
        for (int row = 0; row < matrix.Length; ++row) {
            var stack = new Stack<int>();
            for (int col = 0; col <= matrix[row].Length; ++col) {
                // Set value
                if (col < matrix[row].Length) {
                    if (matrix[row][col] == '1') {
                        histogram[col] += 1;
                    } else {
                        histogram[col] = 0;
                    }
                }
 
                // Compute area
                while (stack.Count > 0 && histogram[stack.Peek()] >= histogram[col]) {
                    var area = histogram[stack.Pop()] * (stack.Count == 0 ? col : (col - stack.Peek() - 1));
                    result = Math.Max(result, area);
                }
                stack.Push(col);
            }
        }
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

6 0 0 1 0

C# || How To Find The Largest Component Size By Common Factor Using C#

November 28, 2021 admin No comments

The following is a module with functions which demonstrates how to find the largest component size by common factor using C#.

1. Largest Component Size – Problem Statement

You are given an integer array of unique positive integers nums. Consider the following graph:

There are nums.length nodes, labeled nums[0] to nums[nums.length – 1],
There is an undirected edge between nums[i] and nums[j] if nums[i] and nums[j] share a common factor greater than 1.

Return the size of the largest connected component in the graph.

Example 1:

Input: nums = [4,6,15,35] Output: 4

Example 2:

Input: nums = [20,50,9,63] Output: 2

Example 3:

Input: nums = [2,3,6,7,4,12,21,39] Output: 8

2. Largest Component Size – Solution

The following is a solution which demonstrates how to find the largest component size by common factor.

The following solution uses a union find set to group connections together.





		
		
			2. Largest Component Size - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 28, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find largest common factor
// ============================================================================
public class Solution {
    public int LargestComponentSize(int[] nums) {
        var set = new UnionFindSet(nums.Max() + 1);

        // Calculate primes set for all elements
        foreach (var num in nums) {
            for (var k = 2; k * k <= num; ++k) {
                if (num % k == 0) {
                    set.Union(num, k);
                    set.Union(num, num / k);
                }
            }
        }

        // Count the apperance of parents, return the maxium one.
        // All connected nodes will point to same parent
        var map = new Dictionary<int, int>();
        var result = 1;
        foreach (var num in nums) {
            var count = set.Find(num);
            map[count] = (map.ContainsKey(count) ? map[count] : 0) + 1;
            result = Math.Max(result, map[count]);
        }
        return result;
    }

    public class UnionFindSet {
        private int[] parent;

        public UnionFindSet(int size) {
            parent = new int[size];
            for (int i = 0; i < parent.Length; ++i) {
                parent[i] = i;
            }
        }
        public void Union(int x, int y) {
            parent[Find(x)] = parent[Find(y)];
        }
        public int Find(int x) {
            if (parent[x] != x) {
                parent[x] = Find(parent[x]);
            }
            return parent[x];
        }
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 28, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find largest common factor
// ============================================================================
public class Solution {
    public int LargestComponentSize(int[] nums) {
        var set = new UnionFindSet(nums.Max() + 1);
 
        // Calculate primes set for all elements
        foreach (var num in nums) {
            for (var k = 2; k * k <= num; ++k) {
                if (num % k == 0) {
                    set.Union(num, k);
                    set.Union(num, num / k);
                }
            }
        }
 
        // Count the apperance of parents, return the maxium one.
        // All connected nodes will point to same parent
        var map = new Dictionary<int, int>();
        var result = 1;
        foreach (var num in nums) {
            var count = set.Find(num);
            map[count] = (map.ContainsKey(count) ? map[count] : 0) + 1;
            result = Math.Max(result, map[count]);
        }
        return result;
    }
 
    public class UnionFindSet {
        private int[] parent;
 
        public UnionFindSet(int size) {
            parent = new int[size];
            for (int i = 0; i < parent.Length; ++i) {
                parent[i] = i;
            }
        }
        public void Union(int x, int y) {
            parent[Find(x)] = parent[Find(y)];
        }
        public int Find(int x) {
            if (parent[x] != x) {
                parent[x] = Find(parent[x]);
            }
            return parent[x];
        }
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

4 2 8

C# || Accounts Merge – How To Merge A List Of Emails Using C#

November 28, 2021 admin No comments

The following is a module with functions which demonstrates how to merge a list of emails using C#.

1. Accounts Merge – Problem Statement

Given a list of accounts where each element accounts[i] is a list of strings, where the first element accounts[i][0] is a name, and the rest of the elements are emails representing emails of the account.

Now, we would like to merge these accounts. Two accounts definitely belong to the same person if there is some common email to both accounts. Note that even if two accounts have the same name, they may belong to different people as people could have the same name. A person can have any number of accounts initially, but all of their accounts definitely have the same name.

After merging the accounts, return the accounts in the following format: the first element of each account is the name, and the rest of the elements are emails in sorted order. The accounts themselves can be returned in any order.

Example 1:

Input: accounts = [["John","johnsmith@mail.com","john_newyork@mail.com"],["John","johnsmith@mail.com","john00@mail.com"],["Mary","mary@mail.com"],["John","johnnybravo@mail.com"]] Output: [["John","john00@mail.com","john_newyork@mail.com","johnsmith@mail.com"],["Mary","mary@mail.com"],["John","johnnybravo@mail.com"]] Explanation: The first and second John's are the same person as they have the common email "johnsmith@mail.com". The third John and Mary are different people as none of their email addresses are used by other accounts. We could return these lists in any order, for example the answer [['Mary', 'mary@mail.com'], ['John', 'johnnybravo@mail.com'], ['John', 'john00@mail.com', 'john_newyork@mail.com', 'johnsmith@mail.com']] would still be accepted.

Example 2:

Input: accounts = [["Gabe","Gabe0@m.co","Gabe3@m.co","Gabe1@m.co"],["Kevin","Kevin3@m.co","Kevin5@m.co","Kevin0@m.co"],["Ethan","Ethan5@m.co","Ethan4@m.co","Ethan0@m.co"],["Hanzo","Hanzo3@m.co","Hanzo1@m.co","Hanzo0@m.co"],["Fern","Fern5@m.co","Fern1@m.co","Fern0@m.co"]] Output: [["Ethan","Ethan0@m.co","Ethan4@m.co","Ethan5@m.co"],["Gabe","Gabe0@m.co","Gabe1@m.co","Gabe3@m.co"],["Hanzo","Hanzo0@m.co","Hanzo1@m.co","Hanzo3@m.co"],["Kevin","Kevin0@m.co","Kevin3@m.co","Kevin5@m.co"],["Fern","Fern0@m.co","Fern1@m.co","Fern5@m.co"]]

2. Accounts Merge – Solution

The following is a solution which demonstrates how to merge a list of emails.

The following solution uses a union find set to group accounts with matching emails together.





		
		
			2. Accounts Merge - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 28, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to merge a list of emails
// ============================================================================
public class Solution {
    public IList<IList<string>> AccountsMerge(IList<IList<string>> accounts) {
        var set = new UnionFindSet(accounts.Count);

        // Map email to their component index
        var emailComponents = new Dictionary<string, int>();
        for (int i = 0; i < accounts.Count; ++i) {
            var account = accounts[i];

            for (int j = 1; j < account.Count; ++j) {
                var email = account[j];

                // Assign component group as the account index
                var group = i;
                if (!emailComponents.ContainsKey(email)) {
                    emailComponents[email] = group;
                } else {
                    // Union this group with the previous group of the email
                    set.Union(group, emailComponents[email]);
                }
            }
        }

        // Store emails corresponding to the components parent
        var emailGroups = new Dictionary<int, List<string>>();
        foreach (var email in emailComponents.Keys) {
            var group = emailComponents[email];
            var groupParent = set.Find(group);

            if (!emailGroups.ContainsKey(groupParent)) {
                emailGroups[groupParent] = new List<string>();
            }
            emailGroups[groupParent].Add(email);
        }

        // Sort the emails and add the account name
        var result = new List<IList<string>>();
        foreach (var group in emailGroups.Keys) {
            var emails = emailGroups[group];
            emails.Sort(StringComparer.Ordinal);
            emails.Insert(0, accounts[group][0]);
            result.Add(emails);
        }
        return result;
    }

    public class UnionFindSet {
        int[] parent;
        int[] size;

        public UnionFindSet(int count) {
            parent = new int[count];
            size = new int[count];
            for (int index = 0; index < count; ++index) {
                parent[index] = index;
                size[index] = 1;
            }
        }
        public int Find(int x) {
            if (parent[x] != x) {
                parent[x] = Find(parent[x]);
            }
            return parent[x];
        }
        public void Union(int x, int y) {
            var parentX = Find(x);
            var parentY = Find(y);
            if (parentX == parentY) {
                return;
            }
            if (size[parentX] >= size[parentY]) {
                size[parentX] += size[parentY];
                parent[parentY] = parentX;
            } else {
                size[parentY] += size[parentX];
                parent[parentX] = parentY;
            }
        }
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 28, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to merge a list of emails
// ============================================================================
public class Solution {
    public IList<IList<string>> AccountsMerge(IList<IList<string>> accounts) {
        var set = new UnionFindSet(accounts.Count);
 
        // Map email to their component index
        var emailComponents = new Dictionary<string, int>();
        for (int i = 0; i < accounts.Count; ++i) {
            var account = accounts[i];
 
            for (int j = 1; j < account.Count; ++j) {
                var email = account[j];
 
                // Assign component group as the account index
                var group = i;
                if (!emailComponents.ContainsKey(email)) {
                    emailComponents[email] = group;
                } else {
                    // Union this group with the previous group of the email
                    set.Union(group, emailComponents[email]);
                }
            }
        }
 
        // Store emails corresponding to the components parent
        var emailGroups = new Dictionary<int, List<string>>();
        foreach (var email in emailComponents.Keys) {
            var group = emailComponents[email];
            var groupParent = set.Find(group);
 
            if (!emailGroups.ContainsKey(groupParent)) {
                emailGroups[groupParent] = new List<string>();
            }
            emailGroups[groupParent].Add(email);
        }
 
        // Sort the emails and add the account name
        var result = new List<IList<string>>();
        foreach (var group in emailGroups.Keys) {
            var emails = emailGroups[group];
            emails.Sort(StringComparer.Ordinal);
            emails.Insert(0, accounts[group][0]);
            result.Add(emails);
        }
        return result;
    }
 
    public class UnionFindSet {
        int[] parent;
        int[] size;
 
        public UnionFindSet(int count) {
            parent = new int[count];
            size = new int[count];
            for (int index = 0; index < count; ++index) {
                parent[index] = index;
                size[index] = 1;
            }
        }
        public int Find(int x) {
            if (parent[x] != x) {
                parent[x] = Find(parent[x]);
            }
            return parent[x];
        }
        public void Union(int x, int y) {
            var parentX = Find(x);
            var parentY = Find(y);
            if (parentX == parentY) {
                return;
            }
            if (size[parentX] >= size[parentY]) {
                size[parentX] += size[parentY];
                parent[parentY] = parentX;
            } else {
                size[parentY] += size[parentX];
                parent[parentX] = parentY;
            }
        }
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[["John","john00@mail.com","john_newyork@mail.com","johnsmith@mail.com"],["Mary","mary@mail.com"],["John","johnnybravo@mail.com"]] [["Gabe","Gabe0@m.co","Gabe1@m.co","Gabe3@m.co"],["Kevin","Kevin0@m.co","Kevin3@m.co","Kevin5@m.co"],["Ethan","Ethan0@m.co","Ethan4@m.co","Ethan5@m.co"],["Hanzo","Hanzo0@m.co","Hanzo1@m.co","Hanzo3@m.co"],["Fern","Fern0@m.co","Fern1@m.co","Fern5@m.co"]]

C# || How To Find All Paths From Source To Target In Graph Using C#

November 28, 2021 admin No comments

The following is a module with functions which demonstrates how to find all paths from source to target in a graph using C#.

1. All Paths Source Target – Problem Statement

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n – 1, find all possible paths from node 0 to node n – 1 and return them in any order.

The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

Example 1:

Input: graph = [[1,2],[3],[3],[]] Output: [[0,1,3],[0,2,3]] Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

Example 2:

Input: graph = [[4,3,1],[3,2,4],[3],[4],[]] Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

Example 3:

Input: graph = [[1],[]] Output: [[0,1]]

Example 4:

Input: graph = [[1,2,3],[2],[3],[]] Output: [[0,1,2,3],[0,2,3],[0,3]]

Example 5:

Input: graph = [[1,3],[2],[3],[]] Output: [[0,1,2,3],[0,3]]

2. All Paths Source Target – Solution

The following is a solution which demonstrates how to find all paths from source to target in a graph.

This solution uses Breadth First Search and backtracking when looking for paths.





		
		
			2. All Paths Source Target - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 28, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find all paths in a graph
// ============================================================================
public class Solution {
    public IList<IList<int>> AllPathsSourceTarget(int[][] graph) {
        var result = new List<IList<int>>();
        var queue = new Queue<List<int>>();

        queue.Enqueue(new List<int>{0});

        while (queue.Count > 0) {
            var currentPath = queue.Dequeue();
            var currentNode = currentPath[currentPath.Count - 1];

            if (currentNode == graph.Length - 1) {
                result.Add(currentPath);
            } else {
                foreach (var child in graph[currentNode]) {
                    currentPath.Add(child);
                    queue.Enqueue(new List<int>(currentPath));
                    currentPath.RemoveAt(currentPath.Count - 1);
                }
            }
        }
        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 28, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find all paths in a graph
// ============================================================================
public class Solution {
    public IList<IList<int>> AllPathsSourceTarget(int[][] graph) {
        var result = new List<IList<int>>();
        var queue = new Queue<List<int>>();
 
        queue.Enqueue(new List<int>{0});
 
        while (queue.Count > 0) {
            var currentPath = queue.Dequeue();
            var currentNode = currentPath[currentPath.Count - 1];
 
            if (currentNode == graph.Length - 1) {
                result.Add(currentPath);
            } else {
                foreach (var child in graph[currentNode]) {
                    currentPath.Add(child);
                    queue.Enqueue(new List<int>(currentPath));
                    currentPath.RemoveAt(currentPath.Count - 1);
                }
            }
        }
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[[0,1,3],[0,2,3]] [[0,4],[0,3,4],[0,1,4],[0,1,3,4],[0,1,2,3,4]] [[0,1]] [[0,3],[0,2,3],[0,1,2,3]] [[0,3],[0,1,2,3]]

C# || How To Search In Rotated Sorted Array Using C#

November 26, 2021 admin No comments

The following is a module with functions which demonstrates how to search for a target value in a rotated sorted array using C#.

1. Search – Problem Statement

There is an integer array nums sorted in ascending order (with distinct values).

Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0 Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3 Output: -1

Example 3:

Input: nums = [1], target = 0 Output: -1

2. Search – Solution

The following is a solution which demonstrates how to search for a target value in a rotated sorted array.

The idea of this solution is to use binary search, and for each loop iteration we compare the midpoint element with the right side of the array to determine the search area of where the target element might be.





		
		
			2. Search - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 26, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to search for a target in a rotated array
// ============================================================================
public class Solution {
    public int Search(int[] nums, int target) {
        var lo = 0;
        var hi = nums.Length - 1;

        while (lo <= hi) {
            var mid = lo + (hi - lo) / 2;

            // Target element found
            if (nums[mid] == target) {
                return mid;

            // Midpoint element is greater than right side of array
            } else if (nums[mid] > nums[hi]) {
                // Determine which side of array to adjust
                if (target < nums[mid] && target >= nums[lo]) {
                    hi = mid - 1;
                } else {
                    lo = mid + 1;
                }

            // Midpoint element is less than right side of array
            } else {
                // Determine which side of array to adjust
                if (target > nums[mid] && target <= nums[hi]) {
                    lo = mid + 1;
                } else {
                    hi = mid - 1;
                }
            }
        }
        return -1;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 26, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to search for a target in a rotated array
// ============================================================================
public class Solution {
    public int Search(int[] nums, int target) {
        var lo = 0;
        var hi = nums.Length - 1;
 
        while (lo <= hi) {
            var mid = lo + (hi - lo) / 2;
 
            // Target element found
            if (nums[mid] == target) {
                return mid;
 
            // Midpoint element is greater than right side of array
            } else if (nums[mid] > nums[hi]) {
                // Determine which side of array to adjust
                if (target < nums[mid] && target >= nums[lo]) {
                    hi = mid - 1;
                } else {
                    lo = mid + 1;
                }
 
            // Midpoint element is less than right side of array
            } else {
                // Determine which side of array to adjust
                if (target > nums[mid] && target <= nums[hi]) {
                    lo = mid + 1;
                } else {
                    hi = mid - 1;
                }
            }
        }
        return -1;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

4 -1 -1

C# || How To Find Product Of Array Except Self Using C#

November 26, 2021 admin No comments

The following is a module with functions which demonstrates how to find the product of an array except itself using C#.

1. Product Except Self – Problem Statement

Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].

The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.

You must write an algorithm that runs in O(n) time and without using the division operation.

Example 1:

Input: nums = [1,2,3,4] Output: [24,12,8,6]

Example 2:

Input: nums = [-1,1,0,-3,3] Output: [0,0,9,0,0]

2. Product Except Self – Solution

The following is a solution which demonstrates how to find the product of an array except itself.

In this solution, the product for result[i] is calculated by scanning the input array, and multiplying the numbers that come before the current i, and the numbers that come after the current i.

First, the running product of the numbers that come before the current i is calculated by scanning the array starting from the beginning (prefix).

Then, the running product of the numbers that come after the current i is calculated by scanning the array starting from the end (suffix).





		
		
			2. Product Except Self - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 26, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find product of array except self
// ============================================================================
public class Solution {
    public int[] ProductExceptSelf(int[] nums) {
        var result = new int[nums.Length];

        // Prefix
        var runningPrefix = 1;
        for (int index = 0; index < nums.Length; ++index) {
            result[index] = runningPrefix;
            runningPrefix *= nums[index];
        }

        // Suffix
        var runningSufix = 1;
        for (int index = nums.Length - 1; index >= 0; --index) {
            result[index] *= runningSufix;
            runningSufix *= nums[index];
        }
        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 26, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find product of array except self
// ============================================================================
public class Solution {
    public int[] ProductExceptSelf(int[] nums) {
        var result = new int[nums.Length];
 
        // Prefix
        var runningPrefix = 1;
        for (int index = 0; index < nums.Length; ++index) {
            result[index] = runningPrefix;
            runningPrefix *= nums[index];
        }
 
        // Suffix
        var runningSufix = 1;
        for (int index = nums.Length - 1; index >= 0; --index) {
            result[index] *= runningSufix;
            runningSufix *= nums[index];
        }
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[24,12,8,6] [0,0,9,0,0]

C# || How To Find Interval List Intersections From Two Arrays Using C#

November 23, 2021 admin No comments

The following is a module with functions which demonstrates how to find interval list intersections from two arrays using C#.

1. Interval Intersection – Problem Statement

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [start_i, end_i] and secondList[j] = [start_j, end_j]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

Example 1:

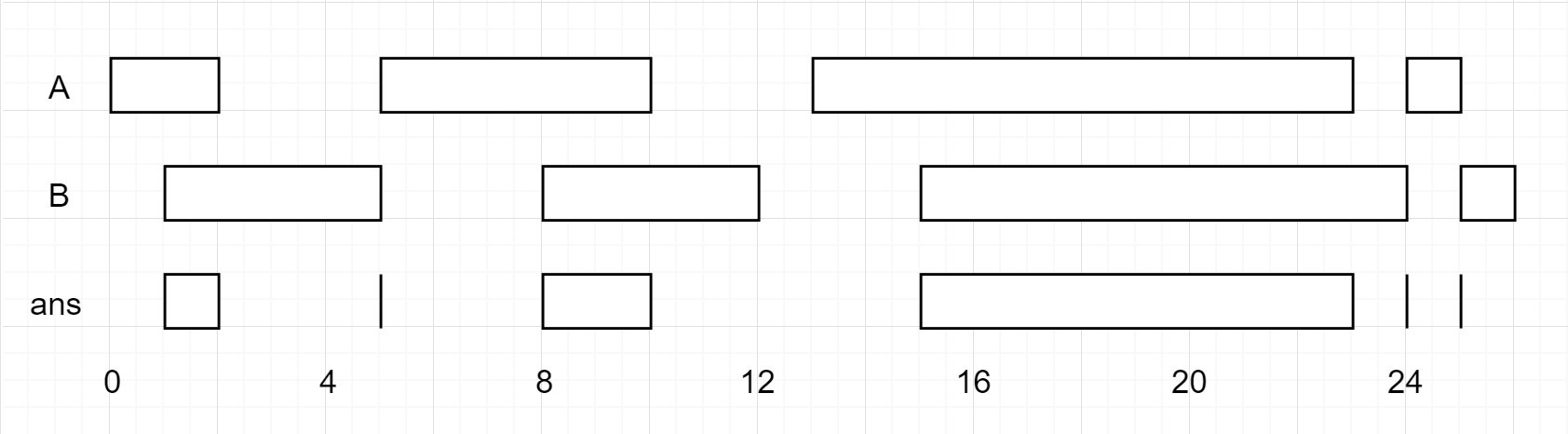
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]] Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Example 2:

Input: firstList = [[1,3],[5,9]], secondList = [] Output: []

Example 3:

Input: firstList = [], secondList = [[4,8],[10,12]] Output: []

Example 4:

Input: firstList = [[1,7]], secondList = [[3,10]] Output: [[3,7]]

2. Interval Intersection – Solution

The following is a solution which demonstrates how to find interval list intersections from two arrays.

This solution uses the two pointer technique when looking for valid interval intersections.





		
		
			2. Interval Intersection - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 23, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find interval list intersections
// ============================================================================
public class Solution {
    public int[][] IntervalIntersection(int[][] firstList, int[][] secondList) {
        var result = new List<int[]>();

        // Go through first and second array looking for range intersection
        var indexFirst = 0;
        var indexSecond = 0;
        while (indexFirst < firstList.Length && indexSecond < secondList.Length) {
            // Get the first and second array
            var first = firstList[indexFirst];
            var second = secondList[indexSecond];

            // Check to see if this is a valid intersection
            if (first[1] >= second[0] && first[0] <= second[1]) {
                // Get starting and ending range from the two arrays
                var start = Math.Max(first[0], second[0]);
                var end = Math.Min(first[1], second[1]);
                result.Add(new int[] {start, end});
            }
            // Increment array index depending on which range is completely satisfied
            if (first[1] < second[1]) {
                ++indexFirst;
            } else {
                ++indexSecond;
            }
        }
        return result.ToArray();
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 23, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find interval list intersections
// ============================================================================
public class Solution {
    public int[][] IntervalIntersection(int[][] firstList, int[][] secondList) {
        var result = new List<int[]>();
 
        // Go through first and second array looking for range intersection
        var indexFirst = 0;
        var indexSecond = 0;
        while (indexFirst < firstList.Length && indexSecond < secondList.Length) {
            // Get the first and second array
            var first = firstList[indexFirst];
            var second = secondList[indexSecond];
 
            // Check to see if this is a valid intersection
            if (first[1] >= second[0] && first[0] <= second[1]) {
                // Get starting and ending range from the two arrays
                var start = Math.Max(first[0], second[0]);
                var end = Math.Min(first[1], second[1]);
                result.Add(new int[] {start, end});
            }
            // Increment array index depending on which range is completely satisfied
            if (first[1] < second[1]) {
                ++indexFirst;
            } else {
                ++indexSecond;
            }
        }
        return result.ToArray();
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]] [] [] [[3,7]]

C# || CombinationIterator – How To Implement Iterator For Combination Using C#

November 20, 2021 admin No comments

The following is a module with functions which demonstrates how to implement iterator for combination using C#.

1. Combination Iterator – Problem Statement

Design the CombinationIterator class:

CombinationIterator(string characters, int combinationLength) Initializes the object with a string characters of sorted distinct lowercase English letters and a number combinationLength as arguments.
next() Returns the next combination of length combinationLength in lexicographical order.
hasNext() Returns true if and only if there exists a next combination.

Example 1:

Input Input: ["CombinationIterator", "next", "hasNext", "next", "hasNext", "next", "hasNext"] [["abc", 2], [], [], [], [], [], []] Output: [null, "ab", true, "ac", true, "bc", false]
Explanation: CombinationIterator itr = new CombinationIterator("abc", 2); itr.next(); // return "ab" itr.hasNext(); // return True itr.next(); // return "ac" itr.hasNext(); // return True itr.next(); // return "bc" itr.hasNext(); // return False

2. Combination Iterator – Solution

The following is a solution which demonstrates how to implement iterator for combination.

The following solution uses backtracking to generate combinations.





		
		
			2. Combination Iterator - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 20, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to implement iterator for combination
// ============================================================================
public class CombinationIterator {
    Queue<string> combinations;

    public CombinationIterator(string characters, int combinationLength) {
        combinations = new Queue<string>();
        Generate(characters, combinationLength, 0, new StringBuilder());
    }

    private void Generate(string characters, int combinationLength, int startIndex, StringBuilder currentCombo) {
        if (currentCombo.Length == combinationLength) {
            combinations.Enqueue(currentCombo.ToString());
            return;
        }

        for (int index = startIndex; index < characters.Length; ++index) {
            // Add this item to the combination
            currentCombo.Append(characters[index]);

            // Keep generating permutations
            Generate(characters, combinationLength, index + 1, currentCombo);

            // Remove last item as its already been explored
            currentCombo.Remove(currentCombo.Length - 1, 1);
        }
    }

    public string Next() {
        return combinations.Dequeue();
    }

    public bool HasNext() {
        return combinations.Count > 0;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 20, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to implement iterator for combination
// ============================================================================
public class CombinationIterator {
    Queue<string> combinations;
 
    public CombinationIterator(string characters, int combinationLength) {
        combinations = new Queue<string>();
        Generate(characters, combinationLength, 0, new StringBuilder());
    }
 
    private void Generate(string characters, int combinationLength, int startIndex, StringBuilder currentCombo) {
        if (currentCombo.Length == combinationLength) {
            combinations.Enqueue(currentCombo.ToString());
            return;
        }
 
        for (int index = startIndex; index < characters.Length; ++index) {
            // Add this item to the combination
            currentCombo.Append(characters[index]);
 
            // Keep generating permutations
            Generate(characters, combinationLength, index + 1, currentCombo);
 
            // Remove last item as its already been explored
            currentCombo.Remove(currentCombo.Length - 1, 1);
        }
    }
 
    public string Next() {
        return combinations.Dequeue();
    }
 
    public bool HasNext() {
        return combinations.Count > 0;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[null,"ab",true,"ac",true,"bc",false]

C# || How To Construct Binary Tree From Preorder And Inorder Traversal Using C#

November 20, 2021 admin No comments

The following is a module with functions which demonstrates how to construct a binary tree from pre order and in order traversal using C#.

1. Build Tree – Problem Statement

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

Example 1:

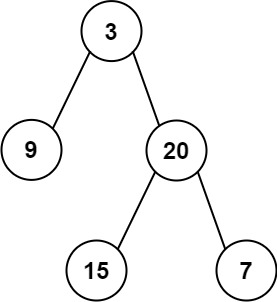
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1] Output: [-1]

2. Build Tree – Solution

The following is a solution which demonstrates how to construct a binary tree from pre order and in order traversal.





		
		
			2. Build Tree - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 20, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to build binary tree from pre order and in order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int preorderIndex;
    private Dictionary<int, int> inorderIndexMap;

    public TreeNode BuildTree(int[] preorder, int[] inorder) {
        preorderIndex = 0;

        // Build a hashmap to store value -> its index relations
        inorderIndexMap = new Dictionary<int, int>();
        for (int index = 0; index < inorder.Length; ++index) {
            inorderIndexMap[inorder[index]] = index;
        }
        return ArrayToTree(preorder, 0, preorder.Length - 1);
    }

    private TreeNode ArrayToTree(int[] preorder, int start, int end) {
        // If there are no elements to construct the tree
        if (start > end) {
            return null;
        }

        // Select the preorder_index element as the root and increment it
        var rootValue = preorder[preorderIndex++];
        var root = new TreeNode(rootValue);

        // Get current positon
        var curPos = inorderIndexMap[rootValue];

        // Build left and right subtree
        // excluding inorderIndexMap[rootValue] element because it's the root
        root.left = ArrayToTree(preorder, start, curPos - 1);
        root.right = ArrayToTree(preorder, curPos + 1, end);
        return root;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 20, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to build binary tree from pre order and in order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int preorderIndex;
    private Dictionary<int, int> inorderIndexMap;
 
    public TreeNode BuildTree(int[] preorder, int[] inorder) {
        preorderIndex = 0;
 
        // Build a hashmap to store value -> its index relations
        inorderIndexMap = new Dictionary<int, int>();
        for (int index = 0; index < inorder.Length; ++index) {
            inorderIndexMap[inorder[index]] = index;
        }
        return ArrayToTree(preorder, 0, preorder.Length - 1);
    }
 
    private TreeNode ArrayToTree(int[] preorder, int start, int end) {
        // If there are no elements to construct the tree
        if (start > end) {
            return null;
        }
 
        // Select the preorder_index element as the root and increment it
        var rootValue = preorder[preorderIndex++];
        var root = new TreeNode(rootValue);
 
        // Get current positon
        var curPos = inorderIndexMap[rootValue];
 
        // Build left and right subtree
        // excluding inorderIndexMap[rootValue] element because it's the root
        root.left = ArrayToTree(preorder, start, curPos - 1);
        root.right = ArrayToTree(preorder, curPos + 1, end);
        return root;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[3,9,20,null,null,15,7] [-1]

C# || How To Construct Binary Tree From Inorder And Postorder Traversal Using C#

November 20, 2021 admin No comments

The following is a module with functions which demonstrates how to construct a binary tree from in order and post order traversal using C#.

1. Build Tree – Problem Statement

Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.

Example 1:

Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] Output: [3,9,20,null,null,15,7]

Example 2:

Input: inorder = [-1], postorder = [-1] Output: [-1]

2. Build Tree – Solution

The following is a solution which demonstrates how to construct a binary tree from in order and post order traversal.





		
		
			2. Build Tree - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 20, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to build binary tree from in order and post order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int postorderIndex;
    private Dictionary<int, int> inorderIndexMap;

    public TreeNode BuildTree(int[] inorder, int[] postorder) {
        postorderIndex = postorder.Length - 1;

        // Build a map to store value & its index relation
        inorderIndexMap = new Dictionary<int, int>();
        for (int index = 0; index < inorder.Length; ++index) {
            inorderIndexMap[inorder[index]] = index;
        }
        return ArrayToTree(postorder, 0, postorder.Length - 1);
    }

    private TreeNode ArrayToTree(int[] postorder, int start, int end) {
        // If there are no elements to construct the tree
        if (start > end) {
            return null;
        }

        // Select the postorder element as the root and decrement it
        var rootValue = postorder[postorderIndex--];
        var root = new TreeNode(rootValue);

        // Get current positon
        var curPos = inorderIndexMap[rootValue];

        // Build left and right subtree
        // excluding inorderIndexMap[rootValue] element because it's the root
        root.right = ArrayToTree(postorder, curPos + 1, end);
        root.left = ArrayToTree(postorder, start, curPos - 1);
        return root;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 20, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to build binary tree from in order and post order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int postorderIndex;
    private Dictionary<int, int> inorderIndexMap;
 
    public TreeNode BuildTree(int[] inorder, int[] postorder) {
        postorderIndex = postorder.Length - 1;
 
        // Build a map to store value & its index relation
        inorderIndexMap = new Dictionary<int, int>();
        for (int index = 0; index < inorder.Length; ++index) {
            inorderIndexMap[inorder[index]] = index;
        }
        return ArrayToTree(postorder, 0, postorder.Length - 1);
    }
 
    private TreeNode ArrayToTree(int[] postorder, int start, int end) {
        // If there are no elements to construct the tree
        if (start > end) {
            return null;
        }
 
        // Select the postorder element as the root and decrement it
        var rootValue = postorder[postorderIndex--];
        var root = new TreeNode(rootValue);
 
        // Get current positon
        var curPos = inorderIndexMap[rootValue];
 
        // Build left and right subtree
        // excluding inorderIndexMap[rootValue] element because it's the root
        root.right = ArrayToTree(postorder, curPos + 1, end);
        root.left = ArrayToTree(postorder, start, curPos - 1);
        return root;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[3,9,20,null,null,15,7] [-1]

C# || How To Find Single Element In A Sorted Array Using C#

November 19, 2021 admin No comments

The following is a module with functions which demonstrates how to find a single element in a sorted array using C#.

1. Single Non Duplicate – Problem Statement

You are given a sorted array consisting of only integers where every element appears exactly twice, except for one element which appears exactly once.

Return the single element that appears only once.

Your solution must run in O(log n) time and O(1) space.

Example 1:

Input: nums = [1,1,2,3,3,4,4,8,8] Output: 2

Example 2:

Input: nums = [3,3,7,7,10,11,11] Output: 10

2. Single Non Duplicate – Solution

The following is a solution which demonstrates how to find a single element in a sorted array.

The idea of this solution is the following:

Suppose we have the following array: [1,1,2,2,3,3,4,4,6,8,8]

We can observe that for each pair:

The first pair element takes the even array index position The second pair element takes the odd array index position

For example, when examining the number 1 as a pair, we see it takes the array index positions 0 and 1.

Similarly for all other pairs, the first pair element takes the even array index position, and the second pair element takes the odd array index position.

Using this idea, we can see that this pattern for pairs will break when a single element appears in the array.

In this solution, we use binary search to look for the point in the array where the pattern mentioned above for the pairs first breaks





		
		
			2. Single Non Duplicate - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 19, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find a single element in a sorted array
// ============================================================================
public class Solution {
    public int SingleNonDuplicate(int[] nums) {
        var lo = 0;
        var hi = nums.Length - 1;

        while (lo < hi) {
            // Get the mipoint
            var mid = lo + (hi - lo) / 2;

            // Check to see if mid is even
            var isEven = mid % 2 == 0;

            // If mid is even, its duplicate should be the next index
            // If mid is odd, its duplicate should be the previous index
            if ((isEven && nums[mid] == nums[mid + 1]) || (!isEven && nums[mid] == nums[mid - 1])) {
                // Duplicate found, advance to next index. Single element is > mid
                lo = mid + 1;
            } else {
                // Pattern is broken. Single element is <= mid
                hi = mid;
            }
        }
        return nums[lo];
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 19, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find a single element in a sorted array
// ============================================================================
public class Solution {
    public int SingleNonDuplicate(int[] nums) {
        var lo = 0;
        var hi = nums.Length - 1;
 
        while (lo < hi) {
            // Get the mipoint
            var mid = lo + (hi - lo) / 2;
 
            // Check to see if mid is even
            var isEven = mid % 2 == 0;
 
            // If mid is even, its duplicate should be the next index
            // If mid is odd, its duplicate should be the previous index
            if ((isEven && nums[mid] == nums[mid + 1]) || (!isEven && nums[mid] == nums[mid - 1])) {
                // Duplicate found, advance to next index. Single element is > mid
                lo = mid + 1;
            } else {
                // Pattern is broken. Single element is <= mid
                hi = mid;
            }
        }
        return nums[lo];
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

2 10

C# || How To Find The Largest Divisible Subset In Array Using C#

November 14, 2021 admin No comments

The following is a module with functions which demonstrates how to find the largest divisible subset in an array using C#.

1. Largest Divisible Subset – Problem Statement

Given a set of distinct positive integers nums, return the largest subset answer such that every pair (answer[i], answer[j]) of elements in this subset satisfies:

answer[i] % answer[j] == 0, or
answer[j] % answer[i] == 0

If there are multiple solutions, return any of them.

Example 1:

Input: nums = [1,2,3] Output: [1,2] Explanation: [1,3] is also accepted.

Example 2:

Input: nums = [1,2,4,8] Output: [1,2,4,8]

2. Largest Divisible Subset – Solution

The following is a solution which demonstrates how to find the largest divisible subset in an array.

This solution uses Dynamic Programming to find the largest divisible subset.





		
		
			2. Largest Divisible Subset - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 14, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the largest divisible subset
// ============================================================================
public class Solution {
    public IList<int> LargestDivisibleSubset(int[] nums) {
        // Sort the array
        Array.Sort(nums);

        // List array of size n
        var dp = new List<int>[nums.Length];

        // Go through numbers
        var resultIndex = 0;
        for (int i = 0; i < nums.Length; ++i) {
            dp[i] = new List<int>();

            // Go through numbers that come before i and determine the maximum subset for i
            var currentMaxIndex = i;
            for (int j = 0; j < i; ++j) {
                // Check if the two numbers satisfies the condition
                if ((nums[i] % nums[j] == 0 || nums[j] % nums[i] == 0) && dp[currentMaxIndex].Count < dp[j].Count) {
                    currentMaxIndex = j;
                }
            }
            // Save items from max index to current dp index
            if (currentMaxIndex != i) {
                dp[i] = new List<int>(dp[currentMaxIndex]);
            }

            // Add current number to current dp index
            dp[i].Add(nums[i]);

            // Keep track of the largest subset
            if (dp[i].Count > dp[resultIndex].Count) {
                resultIndex = i;
            }
        }
        return dp[resultIndex];
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 14, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the largest divisible subset
// ============================================================================
public class Solution {
    public IList<int> LargestDivisibleSubset(int[] nums) {
        // Sort the array
        Array.Sort(nums);
 
        // List array of size n
        var dp = new List<int>[nums.Length];
 
        // Go through numbers
        var resultIndex = 0;
        for (int i = 0; i < nums.Length; ++i) {
            dp[i] = new List<int>();
 
            // Go through numbers that come before i and determine the maximum subset for i
            var currentMaxIndex = i;
            for (int j = 0; j < i; ++j) {
                // Check if the two numbers satisfies the condition
                if ((nums[i] % nums[j] == 0 || nums[j] % nums[i] == 0) && dp[currentMaxIndex].Count < dp[j].Count) {
                    currentMaxIndex = j;
                }
            }
            // Save items from max index to current dp index
            if (currentMaxIndex != i) {
                dp[i] = new List<int>(dp[currentMaxIndex]);
            }
 
            // Add current number to current dp index
            dp[i].Add(nums[i]);
 
            // Keep track of the largest subset
            if (dp[i].Count > dp[resultIndex].Count) {
                resultIndex = i;
            }
        }
        return dp[resultIndex];
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[1,2] [1,2,4,8]

C# || Online Stock Span – How To Get Daily Price Stock Quotes & Consecutive Day Span Using C#

November 12, 2021 admin No comments

The following is a module with functions which demonstrates how to get the daily price stock quotes & consecutive day span using C#.

1. Stock Spanner – Problem Statement

Design an algorithm that collects daily price quotes for some stock and returns the span of that stock’s price for the current day.

The span of the stock’s price today is defined as the maximum number of consecutive days (starting from today and going backward) for which the stock price was less than or equal to today’s price.

For example, if the price of a stock over the next 7 days were [100,80,60,70,60,75,85], then the stock spans would be [1,1,1,2,1,4,6].

Implement the StockSpanner class:

StockSpanner() Initializes the object of the class.
int next(int price) Returns the span of the stock’s price given that today’s price is price.

Example 1:

Input: ["StockSpanner", "next", "next", "next", "next", "next", "next", "next"] [[], [100], [80], [60], [70], [60], [75], [85]] Output: [null, 1, 1, 1, 2, 1, 4, 6]
Explanation: StockSpanner stockSpanner = new StockSpanner(); stockSpanner.next(100); // return 1 stockSpanner.next(80); // return 1 stockSpanner.next(60); // return 1 stockSpanner.next(70); // return 2 stockSpanner.next(60); // return 1 stockSpanner.next(75); // return 4, because the last 4 prices (including today's price of 75) were less than or equal to today's price. stockSpanner.next(85); // return 6

2. Stock Spanner – Solution

The following is a solution which demonstrates how to get the daily price stock quotes & consecutive day span.

This solution uses the monotonic stack approach.

The idea of this solution is to have a stack of a pair to store the current price and the maximum number of consecutive days.

For each new price, we check the top of the stack and keep a running total of each previous consecutive day span found for all stock prices that are less than or equal to today’s price.

Then, we add today’s price and the current running consecutive day total to the stack.





		
		
			2. Stock Spanner - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 12, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the daily price stock quotes day span
// ============================================================================
public class StockSpanner {
    // Store the current price & maximum number of consecutive days
    Stack<KeyValuePair<int, int>> stack;

    public StockSpanner() {
        stack = new Stack<KeyValuePair<int, int>>();
    }

    public int Next(int price) {
        var consecutiveDays = 1;

        // Compare current price with the item on the top of the stack
        while (stack.Count > 0 && stack.Peek().Key <= price) {
            // Get the previous consecutive day span and add to the current result
            consecutiveDays += stack.Peek().Value;
            stack.Pop();
        }
        // Add the current price and consecutive day span to the stack
        stack.Push(new KeyValuePair<int, int>(price, consecutiveDays));

        return consecutiveDays;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 12, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the daily price stock quotes day span
// ============================================================================
public class StockSpanner {
    // Store the current price & maximum number of consecutive days
    Stack<KeyValuePair<int, int>> stack;
 
    public StockSpanner() {
        stack = new Stack<KeyValuePair<int, int>>();
    }
 
    public int Next(int price) {
        var consecutiveDays = 1;
 
        // Compare current price with the item on the top of the stack
        while (stack.Count > 0 && stack.Peek().Key <= price) {
            // Get the previous consecutive day span and add to the current result
            consecutiveDays += stack.Peek().Value;
            stack.Pop();
        }
        // Add the current price and consecutive day span to the stack
        stack.Push(new KeyValuePair<int, int>(price, consecutiveDays));
 
        return consecutiveDays;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[null,1,1,1,2,1,4,6]

Monthly Archives: November 2021

C# || String To Integer (atoi) – How To Convert String To Signed Integer Using C#

C# || Maximal Rectangle – How To Find Largest Rectangle Area Using C#

C# || How To Find The Largest Component Size By Common Factor Using C#

C# || Accounts Merge – How To Merge A List Of Emails Using C#

C# || How To Find All Paths From Source To Target In Graph Using C#

C# || How To Search In Rotated Sorted Array Using C#

C# || How To Find Product Of Array Except Self Using C#

C# || How To Find Interval List Intersections From Two Arrays Using C#

C# || CombinationIterator – How To Implement Iterator For Combination Using C#

C# || How To Construct Binary Tree From Preorder And Inorder Traversal Using C#

C# || How To Construct Binary Tree From Inorder And Postorder Traversal Using C#

C# || How To Find Single Element In A Sorted Array Using C#

C# || How To Find The Largest Divisible Subset In Array Using C#

C# || Online Stock Span – How To Get Daily Price Stock Quotes & Consecutive Day Span Using C#

Search

Compile Your Code Now

Translate Page

Popular Pages

Recent

Archives

Categories