binary tree – My Programming Notes

Tag Archives: binary tree

C# || How To Find Duplicate Subtrees Using C#

April 01, 2025 admin No comments

/js/scroll.js?=1

The following is a module with functions which demonstrates how to find duplicate subtrees using C#.

1. Find Duplicate Subtrees – Problem Statement

Given the root of a binary tree, return all duplicate subtrees.

For each kind of duplicate subtrees, you only need to return the root node of any one of them.

Two trees are duplicate if they have the same structure with the same node values.

Example 1:

Input: root = [1,2,3,4,null,2,4,null,null,4] Output: [[2,4],[4]]

Example 2:

Input: root = [2,1,1] Output: [[1]]

Example 3:

Input: root = [2,2,2,3,null,3,null] Output: [[2,3],[3]]

2. Find Duplicate Subtrees – Solution

The following is a solution which demonstrates how to find duplicate subtrees.





		
		
			2. Find Duplicate Subtrees - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Apr 1, 2025
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find duplicate subtrees
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public IList<TreeNode> FindDuplicateSubtrees(TreeNode root) {
        var result = new List<TreeNode>();
        Traverse(root, new Dictionary<string, int>(), new Dictionary<int, int>(), result);
        return result;
    }

    public int Traverse(TreeNode node, Dictionary<string, int> tripletToID,
            Dictionary<int, int> cnt, List<TreeNode> result) {
        if (node == null) {
            return 0;
        }
        string triplet = Traverse(node.left, tripletToID, cnt, result) + "," + node.val +
                "," + Traverse(node.right, tripletToID, cnt, result);
        if (!tripletToID.ContainsKey(triplet)) {
            tripletToID[triplet] = tripletToID.Count + 1;
        }
        int id = tripletToID[triplet];
        cnt[id] = cnt.GetValueOrDefault(id, 0) + 1;
        if (cnt[id] == 2) {
            result.Add(node);
        }
        return id;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Apr 1, 2025
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find duplicate subtrees
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public IList<TreeNode> FindDuplicateSubtrees(TreeNode root) {
        var result = new List<TreeNode>();
        Traverse(root, new Dictionary<string, int>(), new Dictionary<int, int>(), result);
        return result;
    }
 
    public int Traverse(TreeNode node, Dictionary<string, int> tripletToID,
            Dictionary<int, int> cnt, List<TreeNode> result) {
        if (node == null) {
            return 0;
        }
        string triplet = Traverse(node.left, tripletToID, cnt, result) + "," + node.val +
                "," + Traverse(node.right, tripletToID, cnt, result);
        if (!tripletToID.ContainsKey(triplet)) {
            tripletToID[triplet] = tripletToID.Count + 1;
        }
        int id = tripletToID[triplet];
        cnt[id] = cnt.GetValueOrDefault(id, 0) + 1;
        if (cnt[id] == 2) {
            result.Add(node);
        }
        return id;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[[2,4],[4]] [[1]] [[2,3],[3]]

C# || How To Determine If A Binary Tree Is Even Odd Tree Using C#

March 01, 2024 admin No comments

The following is a module with functions which demonstrates how to determine if a binary tree is an even odd tree using C#.

1. Is Even Odd Tree – Problem Statement

A binary tree is named Even-Odd if it meets the following conditions:

The root of the binary tree is at level index 0, its children are at level index 1, their children are at level index 2, etc.
For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).

Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.

Example 1:

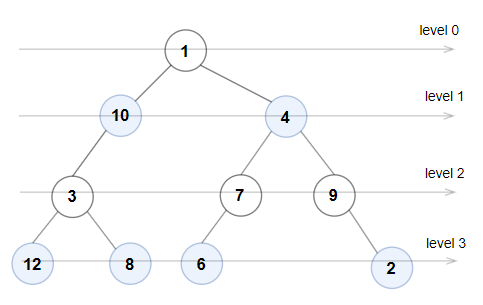
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2] Output: true Explanation: The node values on each level are: Level 0: [1] Level 1: [10,4] Level 2: [3,7,9] Level 3: [12,8,6,2] Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.

Example 2:

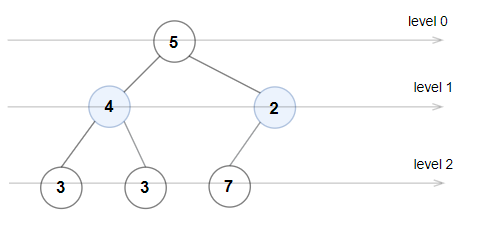
Input: root = [5,4,2,3,3,7] Output: false Explanation: The node values on each level are: Level 0: [5] Level 1: [4,2] Level 2: [3,3,7] Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.

Example 3:

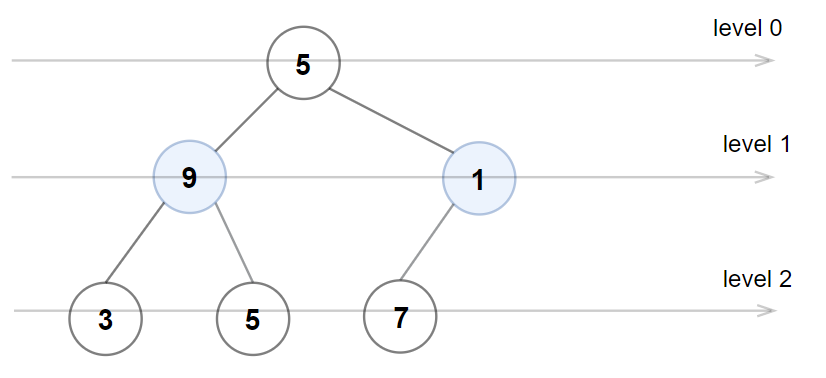
Input: root = [5,9,1,3,5,7] Output: false Explanation: Node values in the level 1 should be even integers.

2. Is Even Odd Tree – Solution

The following is a solution which demonstrates how to determine if a binary tree is an even odd tree.

This solution uses breadth-first search.





		
		
			2. Is Even Odd Tree - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Mar 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to determine an even odd tree
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public bool IsEvenOddTree(TreeNode root) {
        var queue = new Queue<TreeNode>();
        queue.Enqueue(root);

        var isEvenLevel = true;
        while (queue.Count > 0) {
            int previousValue = isEvenLevel ? int.MinValue : int.MaxValue;
            for (var size = queue.Count - 1; size >= 0; --size) {
                var currentNode = queue.Dequeue();

                if (isEvenLevel) {
                    if (IsEven(currentNode.val) || previousValue >= currentNode.val) {
                        return false;
                    }
                } else {
                    if (!IsEven(currentNode.val) || previousValue <= currentNode.val) {
                        return false;
                    }
                }
                if (currentNode.left != null) {
                    queue.Enqueue(currentNode.left);
                }
                if (currentNode.right != null) {
                    queue.Enqueue(currentNode.right);
                }
                previousValue = currentNode.val;
            }
            isEvenLevel = !isEvenLevel;
        }
        return true;
    }

    private bool IsEven(int value) {
        return value % 2 == 0;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Mar 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to determine an even odd tree
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public bool IsEvenOddTree(TreeNode root) {
        var queue = new Queue<TreeNode>();
        queue.Enqueue(root);
 
        var isEvenLevel = true;
        while (queue.Count > 0) {
            int previousValue = isEvenLevel ? int.MinValue : int.MaxValue;
            for (var size = queue.Count - 1; size >= 0; --size) {
                var currentNode = queue.Dequeue();
 
                if (isEvenLevel) {
                    if (IsEven(currentNode.val) || previousValue >= currentNode.val) {
                        return false;
                    }
                } else {
                    if (!IsEven(currentNode.val) || previousValue <= currentNode.val) {
                        return false;
                    }
                }
                if (currentNode.left != null) {
                    queue.Enqueue(currentNode.left);
                }
                if (currentNode.right != null) {
                    queue.Enqueue(currentNode.right);
                }
                previousValue = currentNode.val;
            }
            isEvenLevel = !isEvenLevel;
        }
        return true;
    }
 
    private bool IsEven(int value) {
        return value % 2 == 0;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

true false false

C# || Parallel Courses III – How To Find Minimum Number Months To Complete All Courses Using C#

November 01, 2023 admin No comments

The following is a module with functions which demonstrates how to find the minimum number of months needed to complete all courses using C#.

1. Minimum Time – Problem Statement

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given a 2D integer array relations where relations[j] = [prevCourse_j, nextCourse_j] denotes that course prevCourse_j has to be completed before course nextCourse_j (prerequisite relationship). Furthermore, you are given a 0-indexed integer array time where time[i] denotes how many months it takes to complete the (i+1)^th course.

You must find the minimum number of months needed to complete all the courses following these rules:

You may start taking a course at any time if the prerequisites are met.
Any number of courses can be taken at the same time.

Return the minimum number of months needed to complete all the courses.

Note: The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).

Example 1:

Input: n = 3, relations = [[1,3],[2,3]], time = [3,2,5] Output: 8 Explanation: The figure above represents the given graph and the time required to complete each course. We start course 1 and course 2 simultaneously at month 0. Course 1 takes 3 months and course 2 takes 2 months to complete respectively. Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.

Example 2:

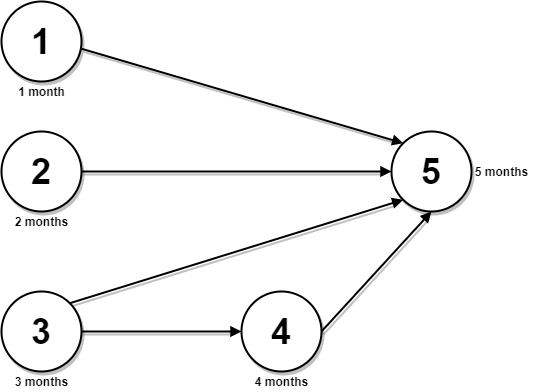
Input: n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5] Output: 12 Explanation: The figure above represents the given graph and the time required to complete each course. You can start courses 1, 2, and 3 at month 0. You can complete them after 1, 2, and 3 months respectively. Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months. Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months. Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.

2. Minimum Time – Solution

The following is a solution which demonstrates how to find the minimum number of months needed to complete all courses.





		
		
			2. Minimum Time - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 1, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the minimum months complete courses
// ============================================================================
public class Solution {
    public int MinimumTime(int n, int[][] relations, int[] time) {
        var graph = new Dictionary<int, List<int>>();
        for (int i = 0; i < n; i++) {
            graph[i] = new List<int>();
        }

        int[] indegree = new int[n];
        foreach (int[] edge in relations) {
            int x = edge[0] - 1;
            int y = edge[1] - 1;
            graph[x].Add(y);
            indegree[y]++;
        }

        var queue = new Queue<int>();
        int[] maxTime = new int[n];

        for (int node = 0; node < n; node++) {
            if (indegree[node] == 0) {
                queue.Enqueue(node);
                maxTime[node] = time[node];
            }
        }

        while (queue.Count > 0) {
            int node = queue.Dequeue();
            foreach (int neighbor in graph[node]) {
                maxTime[neighbor] = Math.Max(maxTime[neighbor], maxTime[node] + time[neighbor]);
                indegree[neighbor]--;
                if (indegree[neighbor] == 0) {
                    queue.Enqueue(neighbor);
                }
            }
        }

        int ans = 0;
        for (int node = 0; node < n; node++) {
            ans = Math.Max(ans, maxTime[node]);
        }

        return ans;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 1, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the minimum months complete courses
// ============================================================================
public class Solution {
    public int MinimumTime(int n, int[][] relations, int[] time) {
        var graph = new Dictionary<int, List<int>>();
        for (int i = 0; i < n; i++) {
            graph[i] = new List<int>();
        }
 
        int[] indegree = new int[n];
        foreach (int[] edge in relations) {
            int x = edge[0] - 1;
            int y = edge[1] - 1;
            graph[x].Add(y);
            indegree[y]++;
        }
 
        var queue = new Queue<int>();
        int[] maxTime = new int[n];
 
        for (int node = 0; node < n; node++) {
            if (indegree[node] == 0) {
                queue.Enqueue(node);
                maxTime[node] = time[node];
            }
        }
 
        while (queue.Count > 0) {
            int node = queue.Dequeue();
            foreach (int neighbor in graph[node]) {
                maxTime[neighbor] = Math.Max(maxTime[neighbor], maxTime[node] + time[neighbor]);
                indegree[neighbor]--;
                if (indegree[neighbor] == 0) {
                    queue.Enqueue(neighbor);
                }
            }
        }
 
        int ans = 0;
        for (int node = 0; node < n; node++) {
            ans = Math.Max(ans, maxTime[node]);
        }
 
        return ans;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

8 12

C# || How To Find Largest Value In Each Binary Tree Row Using C#

October 28, 2023 admin No comments

The following is a module with functions which demonstrates how to find the largest value in each binary tree row using C#.

1. Largest Values – Problem Statement

Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).

Example 1:

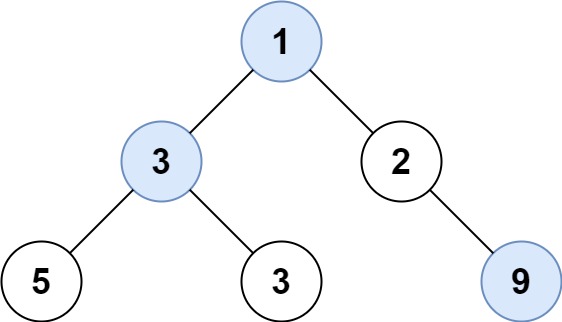
Input: root = [1,3,2,5,3,null,9] Output: [1,3,9]

Example 2:

Input: root = [1,2,3] Output: [1,3]

2. Largest Values – Solution

The following is a solution which demonstrates how to find the largest value in each binary tree row.





		
		
			2. Largest Values - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 28, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the largest value binary tree row
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public IList<int> LargestValues(TreeNode root) {
        if (root == null) {
            return new List<int>();
        }

        var ans = new List<int>();
        var queue = new Queue<TreeNode>();
        queue.Enqueue(root);

        while (queue.Count > 0) {
            int currMax = int.MinValue;
            for (int i = queue.Count -1; i >= 0; --i) {
                var node = queue.Dequeue();
                currMax = Math.Max(currMax, node.val);

                if (node.left != null) {
                    queue.Enqueue(node.left);
                }
                if (node.right != null) {
                    queue.Enqueue(node.right);
                }
            }
            ans.Add(currMax);
        }
        return ans;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 28, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the largest value binary tree row
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public IList<int> LargestValues(TreeNode root) {
        if (root == null) {
            return new List<int>();
        }
 
        var ans = new List<int>();
        var queue = new Queue<TreeNode>();
        queue.Enqueue(root);
 
        while (queue.Count > 0) {
            int currMax = int.MinValue;
            for (int i = queue.Count -1; i >= 0; --i) {
                var node = queue.Dequeue();
                currMax = Math.Max(currMax, node.val);
 
                if (node.left != null) {
                    queue.Enqueue(node.left);
                }
                if (node.right != null) {
                    queue.Enqueue(node.right);
                }
            }
            ans.Add(currMax);
        }
        return ans;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[1,3,9] [1,3]

C# || How To Find Maximum Difference Between Node and Ancestor In Binary Tree Using C#

February 14, 2023 admin No comments

The following is a module with functions which demonstrates how to find the maximum difference between node and ancestor in binary tree using C#.

1. Max Ancestor Diff – Problem Statement

Given the root of a binary tree, find the maximum value v for which there exist different nodes a and b where v = |a.val – b.val| and a is an ancestor of b.

A node a is an ancestor of b if either: any child of a is equal to b or any child of a is an ancestor of b.

Example 1:

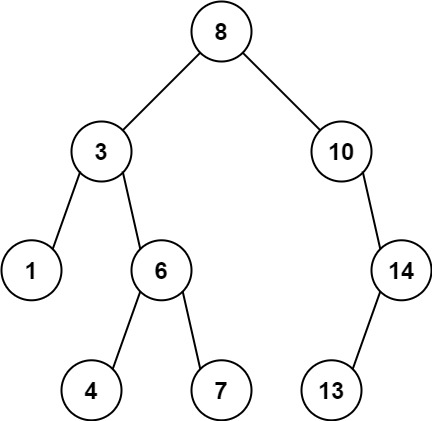
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13] Output: 7 Explanation: We have various ancestor-node differences, some of which are given below : |8 - 3| = 5 |3 - 7| = 4 |8 - 1| = 7 |10 - 13| = 3 Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Example 2:

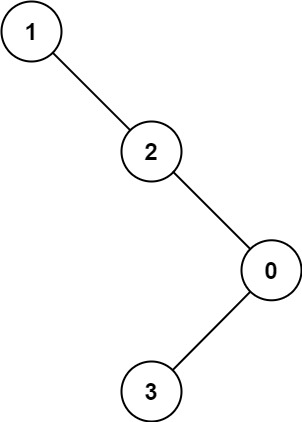
Input: root = [1,null,2,null,0,3] Output: 3

2. Max Ancestor Diff – Solution

The following is a solution which demonstrates how to find the maximum difference between node and ancestor in binary tree.





		
		
			2. Max Ancestor Diff - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Feb 14, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find maximum difference node and ancestor
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int MaxAncestorDiff(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return Traverse(root, root.val, root.val);
    }

    public int Traverse(TreeNode node, int curMax, int curMin) {
        // if encounter leaves, return the max-min along the path
        if (node == null) {
            return curMax - curMin;
        }
        // else, update max and min
        // and return the max of left and right subtrees
        curMax = Math.Max(curMax, node.val);
        curMin = Math.Min(curMin, node.val);
        int left = Traverse(node.left, curMax, curMin);
        int right = Traverse(node.right, curMax, curMin);
        return Math.Max(left, right);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Feb 14, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find maximum difference node and ancestor
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int MaxAncestorDiff(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return Traverse(root, root.val, root.val);
    }
 
    public int Traverse(TreeNode node, int curMax, int curMin) {
        // if encounter leaves, return the max-min along the path
        if (node == null) {
            return curMax - curMin;
        }
        // else, update max and min
        // and return the max of left and right subtrees
        curMax = Math.Max(curMax, node.val);
        curMin = Math.Min(curMin, node.val);
        int left = Traverse(node.left, curMax, curMin);
        int right = Traverse(node.right, curMax, curMin);
        return Math.Max(left, right);
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

7 3

C# || Two Sum IV – How To Get Two Numbers In Binary Search Tree Equal To Target Value Using C#

October 09, 2022 admin No comments

The following is a module with functions which demonstrates how to get two numbers in a binary search tree equal to target value using C#.

1. Find Target – Problem Statement

Given the root of a Binary Search Tree and a target number k, return true if there exist two elements in the BST such that their sum is equal to the given target.

Example 1:

Input: root = [5,3,6,2,4,null,7], k = 9 Output: true

Example 2:

Input: root = [5,3,6,2,4,null,7], k = 28 Output: false

2. Find Target – Solution

The following are two solutions which demonstrates how to get two numbers in a binary search tree equal to target value.

Both solutions use a set to keep track of the items already seen.

Each time a new node is encountered, we subtract the target value from the current node value. If the difference amount from subtracting the two numbers exists in the set, a 2 sum combination exists in the tree

1. Recursive

The following solution uses Depth First Search when looking for the target value.





		
		
			2. Find Target - Solution - Recursive
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 9, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get two numbers equal to target value
// ============================================================================
public class Solution {
    public bool FindTarget(TreeNode root, int k) {
        return Traverse(root, k, new HashSet<int>());
    }

    private bool Traverse(TreeNode node, int k, HashSet<int> seen) {
        if (node == null) {
            return false;
        }
        // Get remaining value
        var remaining = k - node.val;

        // Check if remaining value has been seen
        if (seen.Contains(remaining)) {
            return true;
        }
        // Add current node value to items seen
        seen.Add(node.val);

        // Keep traversing left and right looking for 2 sum
        return Traverse(node.left, k, seen) || Traverse(node.right, k, seen);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 9, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get two numbers equal to target value
// ============================================================================
public class Solution {
    public bool FindTarget(TreeNode root, int k) {
        return Traverse(root, k, new HashSet<int>());
    }
 
    private bool Traverse(TreeNode node, int k, HashSet<int> seen) {
        if (node == null) {
            return false;
        }
        // Get remaining value
        var remaining = k - node.val;
 
        // Check if remaining value has been seen
        if (seen.Contains(remaining)) {
            return true;
        }
        // Add current node value to items seen
        seen.Add(node.val);
 
        // Keep traversing left and right looking for 2 sum
        return Traverse(node.left, k, seen) || Traverse(node.right, k, seen);
    }
}// http://programmingnotes.org/

2. Iterative

The following solution uses Breadth First Search when looking for the target value.





		
		
			2. Find Target - Solution - Iterative
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 9, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get two numbers equal to target value
// ============================================================================
public class Solution {
    public bool FindTarget(TreeNode root, int k) {
        if (root == null) {
            return false;
        }
        // Declare stack
        var stack = new Stack<TreeNode>();

        // Keep track of values seen
        var seen = new HashSet<int>();

        // Add root to stack
        stack.Push(root);

        // Loop through items on the stack
        while (stack.Count > 0) {
            // Get current node
            var node = stack.Pop();

            // Get remaining value
            var remaining = k - node.val;

            // Check if remaining value has been seen
            if (seen.Contains(remaining)) {
                return true;
            } else {
                // Keep traversing left and right looking for 2 sum
                if (node.left != null) {
                    stack.Push(node.left);
                }
                if (node.right != null) {
                    stack.Push(node.right);
                }
            }
            // Add current node value to items seen
            seen.Add(node.val);
        }
        return false;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 9, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get two numbers equal to target value
// ============================================================================
public class Solution {
    public bool FindTarget(TreeNode root, int k) {
        if (root == null) {
            return false;
        }
        // Declare stack
        var stack = new Stack<TreeNode>();
 
        // Keep track of values seen
        var seen = new HashSet<int>();
 
        // Add root to stack
        stack.Push(root);
 
        // Loop through items on the stack
        while (stack.Count > 0) {
            // Get current node
            var node = stack.Pop();
 
            // Get remaining value
            var remaining = k - node.val;
 
            // Check if remaining value has been seen
            if (seen.Contains(remaining)) {
                return true;
            } else {
                // Keep traversing left and right looking for 2 sum
                if (node.left != null) {
                    stack.Push(node.left);
                }
                if (node.right != null) {
                    stack.Push(node.right);
                }
            }
            // Add current node value to items seen
            seen.Add(node.val);
        }
        return false;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

true false

C# || How To Traverse N-ary Tree Level Order Using C#

September 05, 2022 admin No comments

The following is a module with functions which demonstrates how to traverse a N-ary Tree level order using C#.

1. Level Order – Problem Statement

Given an n-ary tree, return the level order traversal of its nodes’ values.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

Example 1:

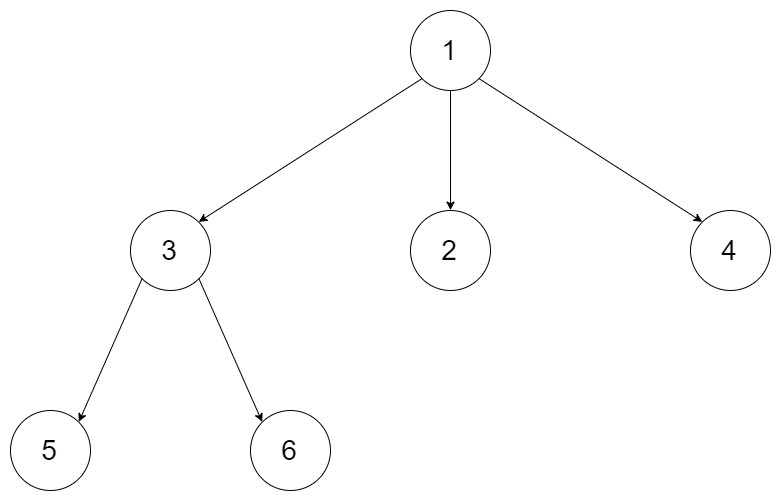
Input: root = [1,null,3,2,4,null,5,6] Output: [[1],[3,2,4],[5,6]]

Example 2:

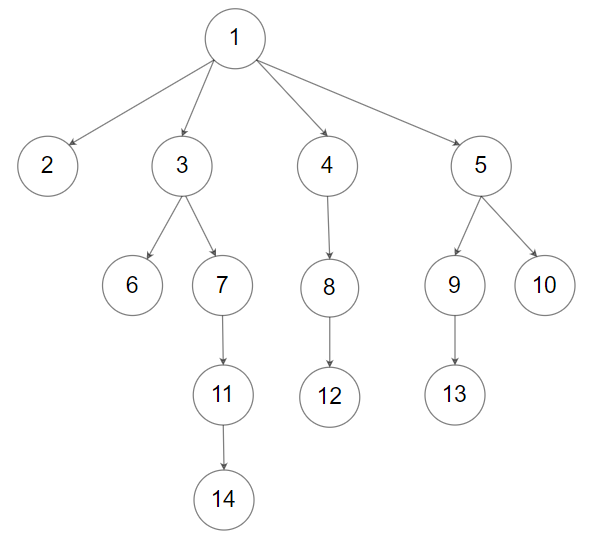
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] Output: [[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

2. Level Order – Solution

The following is a solution which demonstrates how to traverse a N-ary Tree level order.

This solution uses Breadth First Search to explore items at each level.





		
		
			2. Level Order - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Sep 5, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to traverse a N-ary Tree Level Order
// ============================================================================
/*
// Definition for a Node.
public class Node {
    public int val;
    public IList<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, IList<Node> _children) {
        val = _val;
        children = _children;
    }
}
*/
public class Solution {
    public IList<IList<int>> LevelOrder(Node root) {
        var result = new List<IList<int>>();
        if (root == null) {
           return result;
        }

        var queue = new Queue<Node>();
        queue.Enqueue(root);

        while (queue.Count > 0) {
            var currentLevel = new List<int>();
            for (int count = queue.Count - 1; count >= 0 ; --count) {
                var currentNode = queue.Dequeue();
                currentLevel.Add(currentNode.val);
                foreach (var child in currentNode.children) {
                    queue.Enqueue(child);
                }
            }
            result.Add(currentLevel);
        }

        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Sep 5, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to traverse a N-ary Tree Level Order
// ============================================================================
/*
// Definition for a Node.
public class Node {
    public int val;
    public IList<Node> children;
 
    public Node() {}
 
    public Node(int _val) {
        val = _val;
    }
 
    public Node(int _val, IList<Node> _children) {
        val = _val;
        children = _children;
    }
}
*/
public class Solution {
    public IList<IList<int>> LevelOrder(Node root) {
        var result = new List<IList<int>>();
        if (root == null) {
           return result;
        }
 
        var queue = new Queue<Node>();
        queue.Enqueue(root);
 
        while (queue.Count > 0) {
            var currentLevel = new List<int>();
            for (int count = queue.Count - 1; count >= 0 ; --count) {
                var currentNode = queue.Dequeue();
                currentLevel.Add(currentNode.val);
                foreach (var child in currentNode.children) {
                    queue.Enqueue(child);
                }
            }
            result.Add(currentLevel);
        }
 
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[[1],[3,2,4],[5,6]] [[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

C# || How To Validate A Binary Search Tree Using C#

August 12, 2022 admin No comments

The following is a module with functions which demonstrates how to validate a binary search tree using C#.

1. Is Valid BST – Problem Statement

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.

Example 1:

Input: root = [2,1,3] Output: true

Example 2:

Input: root = [5,1,4,null,null,3,6] Output: false Explanation: The root node's value is 5 but its right child's value is 4.

2. Is Valid BST – Solution

The following is a solution which demonstrates how to validate a binary search tree.





		
		
			2. Is Valid BST - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Aug 12, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to validate a BST
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public bool IsValidBST(TreeNode root) {
        return Traverse(root, null, null);
    }

    private bool Traverse(TreeNode node, TreeNode min, TreeNode max) {
        if (node == null) {
            return true;
        }
        if (max != null && node.val >= max.val) {
            return false;
        }
        if (min != null && node.val <= min.val) {
            return false;
        }
        return Traverse(node.left, min, node)
            && Traverse(node.right, node, max);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Aug 12, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to validate a BST
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public bool IsValidBST(TreeNode root) {
        return Traverse(root, null, null);
    }
 
    private bool Traverse(TreeNode node, TreeNode min, TreeNode max) {
        if (node == null) {
            return true;
        }
        if (max != null && node.val >= max.val) {
            return false;
        }
        if (min != null && node.val <= min.val) {
            return false;
        }
        return Traverse(node.left, min, node)
            && Traverse(node.right, node, max);
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

true false

C# || Binary Tree Right Side View – How To Get Nodes Ordered Top To Bottom C#

July 10, 2022 admin No comments

The following is a module with functions which demonstrates how to get nodes in a binary tree ordered from top to bottom using C#.

1. Right Side View – Problem Statement

Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.

Example 1:

Input: root = [1,2,3,null,5,null,4] Output: [1,3,4]

Example 2:

Input: root = [1,null,3] Output: [1,3]

Example 3:

Input: root = [] Output: []

2. Right Side View – Solution

The following is a solution which demonstrates how to get right side nodes ordered from top to bottom.

This solution uses Depth First Search level order traversal to explore items at each level, and then adds the last node on every layer.





		
		
			2. Right Side View - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jul 10, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get nodes ordered from top to bottom
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public IList<int> RightSideView(TreeNode root) {
        var result = new List<int>();
        Traverse(root, 0, result);
        return result;
    }

    public void Traverse(TreeNode node, int currentDepth, List<int> result) {
        if (node == null) {
            return;
        }
        if (currentDepth == result.Count) {
            result.Add(node.val);
        }
        Traverse(node.right, currentDepth + 1, result);
        Traverse(node.left, currentDepth + 1, result);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jul 10, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get nodes ordered from top to bottom
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public IList<int> RightSideView(TreeNode root) {
        var result = new List<int>();
        Traverse(root, 0, result);
        return result;
    }
 
    public void Traverse(TreeNode node, int currentDepth, List<int> result) {
        if (node == null) {
            return;
        }
        if (currentDepth == result.Count) {
            result.Add(node.val);
        }
        Traverse(node.right, currentDepth + 1, result);
        Traverse(node.left, currentDepth + 1, result);
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[1,3,4] [1,3] []

C# || How To Get Total Sum Root To Leaf Binary Numbers In Binary Tree Using C#

January 10, 2022 admin No comments

The following is a module with functions which demonstrates how to get the total sum root to leaf binary numbers in a binary tree using C#.

1. Sum Root To Leaf – Problem Statement

You are given the root of a binary tree where each node has a value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit.

For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.

For all leaves in the tree, consider the numbers represented by the path from the root to that leaf. Return the sum of these numbers.

The test cases are generated so that the answer fits in a 32-bits integer.

A leaf node is a node with no children.

Example 1:

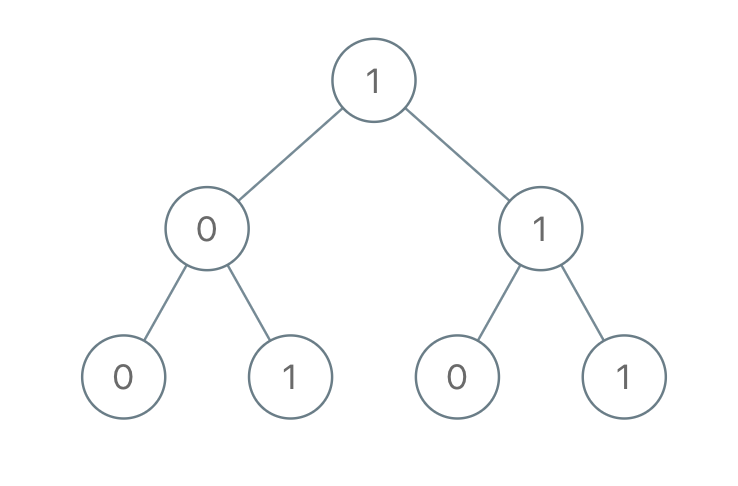
Input: root = [1,0,1,0,1,0,1] Output: 22 Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

Example 2:

Input: root = [0] Output: 0

2. Sum Root To Leaf – Solution

The following is a solution which demonstrates how to get the total sum root to leaf binary numbers in a binary tree.

This solution uses Depth First Search to explore items at each level.





		
		
			2. Sum Root To Leaf - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jan 10, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get sum root to leaf binary numbers
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumRootToLeaf(TreeNode root) {
        return Traverse(root, 0);
    }
    private int Traverse(TreeNode node, int currentSum) {
        if (node == null) {
            return 0;
        }
        // Calculate current sum
        currentSum = (currentSum * 2) + node.val;

        // We have reached a leaf node
        if (node.left == null && node.right == null) {
            return currentSum;
        }
        // Keep traversing left and right calculating the sum
        return Traverse(node.left, currentSum) + Traverse(node.right, currentSum);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jan 10, 2022
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get sum root to leaf binary numbers
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumRootToLeaf(TreeNode root) {
        return Traverse(root, 0);
    }
    private int Traverse(TreeNode node, int currentSum) {
        if (node == null) {
            return 0;
        }
        // Calculate current sum
        currentSum = (currentSum * 2) + node.val;
 
        // We have reached a leaf node
        if (node.left == null && node.right == null) {
            return currentSum;
        }
        // Keep traversing left and right calculating the sum
        return Traverse(node.left, currentSum) + Traverse(node.right, currentSum);
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

22 0

C# || How To Construct Binary Tree From Preorder And Inorder Traversal Using C#

November 20, 2021 admin No comments

The following is a module with functions which demonstrates how to construct a binary tree from pre order and in order traversal using C#.

1. Build Tree – Problem Statement

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

Example 1:

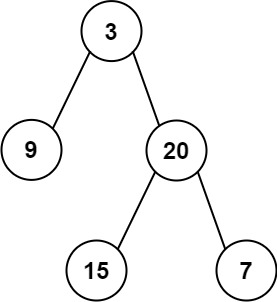
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1] Output: [-1]

2. Build Tree – Solution

The following is a solution which demonstrates how to construct a binary tree from pre order and in order traversal.





		
		
			2. Build Tree - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 20, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to build binary tree from pre order and in order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int preorderIndex;
    private Dictionary<int, int> inorderIndexMap;

    public TreeNode BuildTree(int[] preorder, int[] inorder) {
        preorderIndex = 0;

        // Build a hashmap to store value -> its index relations
        inorderIndexMap = new Dictionary<int, int>();
        for (int index = 0; index < inorder.Length; ++index) {
            inorderIndexMap[inorder[index]] = index;
        }
        return ArrayToTree(preorder, 0, preorder.Length - 1);
    }

    private TreeNode ArrayToTree(int[] preorder, int start, int end) {
        // If there are no elements to construct the tree
        if (start > end) {
            return null;
        }

        // Select the preorder_index element as the root and increment it
        var rootValue = preorder[preorderIndex++];
        var root = new TreeNode(rootValue);

        // Get current positon
        var curPos = inorderIndexMap[rootValue];

        // Build left and right subtree
        // excluding inorderIndexMap[rootValue] element because it's the root
        root.left = ArrayToTree(preorder, start, curPos - 1);
        root.right = ArrayToTree(preorder, curPos + 1, end);
        return root;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 20, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to build binary tree from pre order and in order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int preorderIndex;
    private Dictionary<int, int> inorderIndexMap;
 
    public TreeNode BuildTree(int[] preorder, int[] inorder) {
        preorderIndex = 0;
 
        // Build a hashmap to store value -> its index relations
        inorderIndexMap = new Dictionary<int, int>();
        for (int index = 0; index < inorder.Length; ++index) {
            inorderIndexMap[inorder[index]] = index;
        }
        return ArrayToTree(preorder, 0, preorder.Length - 1);
    }
 
    private TreeNode ArrayToTree(int[] preorder, int start, int end) {
        // If there are no elements to construct the tree
        if (start > end) {
            return null;
        }
 
        // Select the preorder_index element as the root and increment it
        var rootValue = preorder[preorderIndex++];
        var root = new TreeNode(rootValue);
 
        // Get current positon
        var curPos = inorderIndexMap[rootValue];
 
        // Build left and right subtree
        // excluding inorderIndexMap[rootValue] element because it's the root
        root.left = ArrayToTree(preorder, start, curPos - 1);
        root.right = ArrayToTree(preorder, curPos + 1, end);
        return root;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[3,9,20,null,null,15,7] [-1]

C# || How To Construct Binary Tree From Inorder And Postorder Traversal Using C#

November 20, 2021 admin No comments

The following is a module with functions which demonstrates how to construct a binary tree from in order and post order traversal using C#.

1. Build Tree – Problem Statement

Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.

Example 1:

Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] Output: [3,9,20,null,null,15,7]

Example 2:

Input: inorder = [-1], postorder = [-1] Output: [-1]

2. Build Tree – Solution

The following is a solution which demonstrates how to construct a binary tree from in order and post order traversal.





		
		
			2. Build Tree - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 20, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to build binary tree from in order and post order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int postorderIndex;
    private Dictionary<int, int> inorderIndexMap;

    public TreeNode BuildTree(int[] inorder, int[] postorder) {
        postorderIndex = postorder.Length - 1;

        // Build a map to store value & its index relation
        inorderIndexMap = new Dictionary<int, int>();
        for (int index = 0; index < inorder.Length; ++index) {
            inorderIndexMap[inorder[index]] = index;
        }
        return ArrayToTree(postorder, 0, postorder.Length - 1);
    }

    private TreeNode ArrayToTree(int[] postorder, int start, int end) {
        // If there are no elements to construct the tree
        if (start > end) {
            return null;
        }

        // Select the postorder element as the root and decrement it
        var rootValue = postorder[postorderIndex--];
        var root = new TreeNode(rootValue);

        // Get current positon
        var curPos = inorderIndexMap[rootValue];

        // Build left and right subtree
        // excluding inorderIndexMap[rootValue] element because it's the root
        root.right = ArrayToTree(postorder, curPos + 1, end);
        root.left = ArrayToTree(postorder, start, curPos - 1);
        return root;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 20, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to build binary tree from in order and post order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int postorderIndex;
    private Dictionary<int, int> inorderIndexMap;
 
    public TreeNode BuildTree(int[] inorder, int[] postorder) {
        postorderIndex = postorder.Length - 1;
 
        // Build a map to store value & its index relation
        inorderIndexMap = new Dictionary<int, int>();
        for (int index = 0; index < inorder.Length; ++index) {
            inorderIndexMap[inorder[index]] = index;
        }
        return ArrayToTree(postorder, 0, postorder.Length - 1);
    }
 
    private TreeNode ArrayToTree(int[] postorder, int start, int end) {
        // If there are no elements to construct the tree
        if (start > end) {
            return null;
        }
 
        // Select the postorder element as the root and decrement it
        var rootValue = postorder[postorderIndex--];
        var root = new TreeNode(rootValue);
 
        // Get current positon
        var curPos = inorderIndexMap[rootValue];
 
        // Build left and right subtree
        // excluding inorderIndexMap[rootValue] element because it's the root
        root.right = ArrayToTree(postorder, curPos + 1, end);
        root.left = ArrayToTree(postorder, start, curPos - 1);
        return root;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[3,9,20,null,null,15,7] [-1]

C# || How To Get Total Sum Of Left Leaves In Binary Tree Using C#

November 03, 2021 admin No comments

The following is a module with functions which demonstrates how to get the total sum of left leaves in a binary tree using C#.

1. Sum Of Left Leaves – Problem Statement

Given the root of a binary tree, return the sum of all left leaves.

A leaf node is a node with no children.

Example 1:

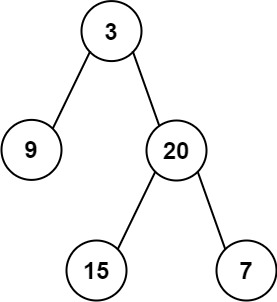
Input: root = [3,9,20,null,null,15,7] Output: 24 Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.

Example 2:

Input: root = [1] Output: 0

2. Sum Of Left Leaves – Solution

The following are two solutions which demonstrates how to get the total sum of left leaves in a binary tree.

Both solutions use Depth First Search to explore items at each level.

In both solutions, we traverse the left and right side of the tree, keeping track of which node is the ‘left’ node.

When a leaf is encountered and its a node on the left side, we increment the final result with the value of the node on the left side.

Recursive





		
		
			2. Sum Of Left Leaves - Recursive - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the sum of left leaves
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumOfLeftLeaves(TreeNode root) {
        return Traverse(root, false);
    }

    private int Traverse(TreeNode node, bool isLeft) {
        if (node == null) {
            return 0;
        }
        // We have reached a leaf node
        if (node.left == null && node.right == null) {
            return isLeft ? node.val : 0;
        }
        // Keep traversing left and right looking for left leaves
        return Traverse(node.left, true) + Traverse(node.right, false);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the sum of left leaves
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumOfLeftLeaves(TreeNode root) {
        return Traverse(root, false);
    }
 
    private int Traverse(TreeNode node, bool isLeft) {
        if (node == null) {
            return 0;
        }
        // We have reached a leaf node
        if (node.left == null && node.right == null) {
            return isLeft ? node.val : 0;
        }
        // Keep traversing left and right looking for left leaves
        return Traverse(node.left, true) + Traverse(node.right, false);
    }
}// http://programmingnotes.org/

Iterative





		
		
			2. Sum Of Left Leaves - Iterative - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the sum of left leaves
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // Declare stack
        var stack = new Stack<KeyValuePair<TreeNode, bool>>();
        var result = 0;

        // Add root to stack
        stack.Push(new KeyValuePair<TreeNode, bool>(root, false));

        // Loop through items on the stack
        while (stack.Count > 0) {
            // Get current node and value indicating if its a left node
            var current = stack.Pop();
            var node = current.Key;
            var isLeft = current.Value;

            // We have reached a leaf node
            if (node.left == null && node.right == null) {
                result += isLeft ? node.val : 0;
            } else {
                // Keep traversing left and right looking for left leaves
                if (node.left != null) {
                    stack.Push(new KeyValuePair<TreeNode, bool>(node.left, true));
                }
                if (node.right != null) {
                    stack.Push(new KeyValuePair<TreeNode, bool>(node.right, false));
                }
            }
        }

        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the sum of left leaves
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // Declare stack
        var stack = new Stack<KeyValuePair<TreeNode, bool>>();
        var result = 0;
 
        // Add root to stack
        stack.Push(new KeyValuePair<TreeNode, bool>(root, false));
 
        // Loop through items on the stack
        while (stack.Count > 0) {
            // Get current node and value indicating if its a left node
            var current = stack.Pop();
            var node = current.Key;
            var isLeft = current.Value;
 
            // We have reached a leaf node
            if (node.left == null && node.right == null) {
                result += isLeft ? node.val : 0;
            } else {
                // Keep traversing left and right looking for left leaves
                if (node.left != null) {
                    stack.Push(new KeyValuePair<TreeNode, bool>(node.left, true));
                }
                if (node.right != null) {
                    stack.Push(new KeyValuePair<TreeNode, bool>(node.right, false));
                }
            }
        }
 
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

24 0

C# || How To Get Total Sum Root To Leaf Numbers In Binary Tree Using C#

November 03, 2021 admin No comments

The following is a module with functions which demonstrates how to get the total sum root to leaf numbers in a binary tree using C#.

1. Sum Numbers – Problem Statement

You are given the root of a binary tree containing digits from 0 to 9 only.

Each root-to-leaf path in the tree represents a number.

For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.

Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.

A leaf node is a node with no children.

Example 1:

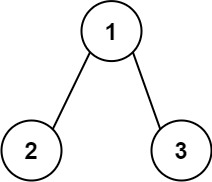
Input: root = [1,2,3] Output: 25 Explanation: The root-to-leaf path 1->2 represents the number 12. The root-to-leaf path 1->3 represents the number 13. Therefore, sum = 12 + 13 = 25.

Example 2:

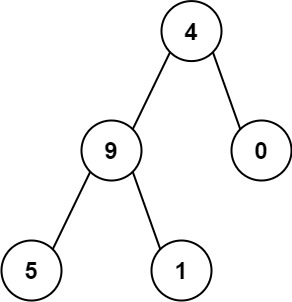
Input: root = [4,9,0,5,1] Output: 1026 Explanation: The root-to-leaf path 4->9->5 represents the number 495. The root-to-leaf path 4->9->1 represents the number 491. The root-to-leaf path 4->0 represents the number 40. Therefore, sum = 495 + 491 + 40 = 1026.

2. Sum Numbers – Solution

The following are two solutions which demonstrates how to get the total sum root to leaf numbers in a binary tree.

Both solutions use Depth First Search to explore items at each level.

Recursive





		
		
			2. Sum Numbers - Recursive - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get sum root to leaf numbers
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumNumbers(TreeNode root) {
        return Traverse(root, 0);
    }

    private int Traverse(TreeNode node, int currentSum) {
        if (node == null) {
            return 0;
        }

        // Calculate current sum
        currentSum = (currentSum * 10) + node.val;

        // We have reached a leaf node
        if (node.left == null && node.right == null) {
            return currentSum;
        }

        // Keep traversing left and right calculating the sum
        return Traverse(node.left, currentSum) + Traverse(node.right, currentSum);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get sum root to leaf numbers
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumNumbers(TreeNode root) {
        return Traverse(root, 0);
    }
 
    private int Traverse(TreeNode node, int currentSum) {
        if (node == null) {
            return 0;
        }
 
        // Calculate current sum
        currentSum = (currentSum * 10) + node.val;
 
        // We have reached a leaf node
        if (node.left == null && node.right == null) {
            return currentSum;
        }
 
        // Keep traversing left and right calculating the sum
        return Traverse(node.left, currentSum) + Traverse(node.right, currentSum);
    }
}// http://programmingnotes.org/

Iterative





		
		
			2. Sum Numbers - Iterative - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get sum root to leaf numbers
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumNumbers(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // Declare stack
        var stack = new Stack<KeyValuePair<TreeNode, int>>();
        var result = 0;

        // Add root to stack
        stack.Push(new KeyValuePair<TreeNode, int>(root, 0));

        // Loop through items on the stack
        while (stack.Count > 0) {
            // Get current node and running sum
            var current = stack.Pop();
            var node = current.Key;
            var currentSum = current.Value;

            // Calculate current sum
            currentSum = (currentSum * 10) + node.val;

            // We have reached a leaf node
            if (node.left == null && node.right == null) {
                result += currentSum;
            } else {
                // Keep traversing left and right calculating the sum
                if (node.left != null) {
                    stack.Push(new KeyValuePair<TreeNode, int>(node.left, currentSum));
                }
                if (node.right != null) {
                    stack.Push(new KeyValuePair<TreeNode, int>(node.right, currentSum));
                }
            }
        }
        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get sum root to leaf numbers
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumNumbers(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // Declare stack
        var stack = new Stack<KeyValuePair<TreeNode, int>>();
        var result = 0;
 
        // Add root to stack
        stack.Push(new KeyValuePair<TreeNode, int>(root, 0));
 
        // Loop through items on the stack
        while (stack.Count > 0) {
            // Get current node and running sum
            var current = stack.Pop();
            var node = current.Key;
            var currentSum = current.Value;
 
            // Calculate current sum
            currentSum = (currentSum * 10) + node.val;
 
            // We have reached a leaf node
            if (node.left == null && node.right == null) {
                result += currentSum;
            } else {
                // Keep traversing left and right calculating the sum
                if (node.left != null) {
                    stack.Push(new KeyValuePair<TreeNode, int>(node.left, currentSum));
                }
                if (node.right != null) {
                    stack.Push(new KeyValuePair<TreeNode, int>(node.right, currentSum));
                }
            }
        }
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

25 1026

Tag Archives: binary tree

C# || How To Find Duplicate Subtrees Using C#

C# || How To Determine If A Binary Tree Is Even Odd Tree Using C#

C# || Parallel Courses III – How To Find Minimum Number Months To Complete All Courses Using C#

C# || How To Find Largest Value In Each Binary Tree Row Using C#

C# || How To Find Maximum Difference Between Node and Ancestor In Binary Tree Using C#

C# || Two Sum IV – How To Get Two Numbers In Binary Search Tree Equal To Target Value Using C#

C# || How To Traverse N-ary Tree Level Order Using C#

C# || How To Validate A Binary Search Tree Using C#

C# || Binary Tree Right Side View – How To Get Nodes Ordered Top To Bottom C#

C# || How To Get Total Sum Root To Leaf Binary Numbers In Binary Tree Using C#

C# || How To Construct Binary Tree From Preorder And Inorder Traversal Using C#

C# || How To Construct Binary Tree From Inorder And Postorder Traversal Using C#

C# || How To Get Total Sum Of Left Leaves In Binary Tree Using C#

C# || How To Get Total Sum Root To Leaf Numbers In Binary Tree Using C#

Search

Compile Your Code Now

Translate Page

Popular Pages

Recent

Archives

Categories