Tag Archives: binary tree
C# || How To Traverse Binary Tree Level Order Using C#

The following is a module with functions which demonstrates how to traverse binary tree level order using C#.
1. Level Order – Problem Statement
Given the root of a binary tree, return the level order traversal of its nodes’ values. (i.e., from left to right, level by level).
Example 1:
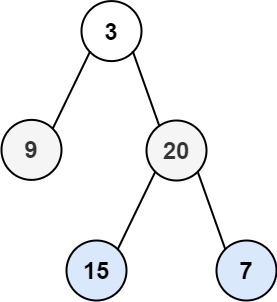
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]
Example 2:
Input: root = [1]
Output: [[1]]
Example 3:
Input: root = []
Output: []
2. Level Order – Solution
The following is a solution which demonstrates how to traverse binary tree level order.
This solution uses Breadth First Search to explore items at each level.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
// ============================================================================// Author: Kenneth Perkins// Date: Oct 29, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Determines how to traverse a tree level order// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { public IList<IList<int>> LevelOrder(TreeNode root) { var result = new List<IList<int>>(); var queue = new Queue<TreeNode>(); if (root != null) { queue.Enqueue(root); } while (queue.Count > 0) { var level = new List<int>(); // Loop through items in the queue for (var itemCount = queue.Count; itemCount > 0; --itemCount) { var current = queue.Peek(); queue.Dequeue(); // Add children to the queue if they exist if (current.left != null) { queue.Enqueue(current.left); } if (current.right != null) { queue.Enqueue(current.right); } // Add current value to the level level.Add(current.val); } // Add items on this level to the result result.Add(level); } return result; }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[[3],[9,20],[15,7]]
[[1]]
[]
C# || How To Invert Binary Tree Using C#

The following is a module with functions which demonstrates how to invert a binary tree using C#.
1. Invert Tree – Problem Statement
Given the root of a binary tree, invert the tree, and return its root.
Example 1:
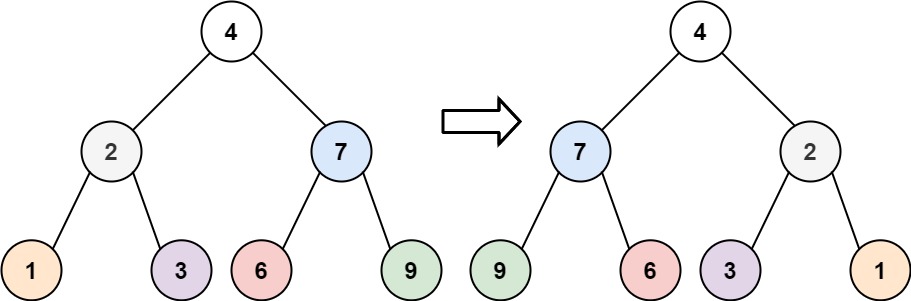
Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]
Example 2:
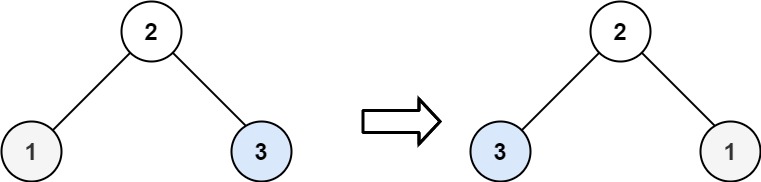
Input: root = [2,1,3]
Output: [2,3,1]
Example 3:
Input: root = []
Output: []
2. Invert Tree – Solution
The following is a solution which demonstrates how to invert a binary tree.
An inverted Binary Tree is simply a Binary Tree whose left and right children are swapped.
This solution:
- Traverses the left subtree
- Traverses the right subtree
- When both trees have been traversed, swap left and right child subtrees
1234567891011121314151617181920212223242526272829303132333435363738394041
// ============================================================================// Author: Kenneth Perkins// Date: Oct 26, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Demonstrates how to invert a binary tree// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { public TreeNode InvertTree(TreeNode root) { Traverse(root); return root; } private void Traverse(TreeNode node) { if (node == null) { return; } // Keep traversing left and right nodes Traverse(node.left); Traverse(node.right); // Root has been visited, swap left and right child nodes var temp = node.left; node.left = node.right; node.right = temp; }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[4,7,2,9,6,3,1]
[2,3,1]
[]
C# || How To Determine Whether A Binary Tree Is A Symmetric Tree Using C#

The following is a module with functions which demonstrates how to determine whether a binary tree is a symmetric tree using C#.
1. Is Symmetric – Problem Statement
Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Example 1:
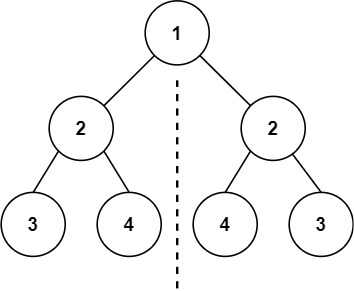
Input: root = [1,2,2,3,4,4,3]
Output: true
Example 2:
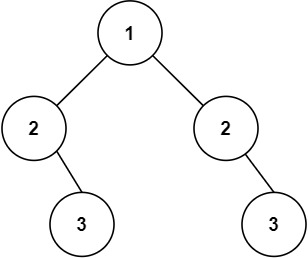
Input: root = [1,2,2,null,3,null,3]
Output: false
2. Is Symmetric – Solution
The following is a solution which demonstrates how to determine whether a binary tree is a symmetric tree.
For two trees to be mirror images, the following three conditions must be true:
• 1 - Their root node's key must be same
• 2 - The left subtree of left tree and right subtree of right tree have to be mirror images
• 3 - The right subtree of left tree and left subtree of right tree have to be mirror images
123456789101112131415161718192021222324252627282930313233343536373839404142
// ============================================================================// Author: Kenneth Perkins// Date: Oct 20, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Determines whether a binary tree is a symmetric tree// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { public bool IsSymmetric(TreeNode root) { return IsMirror(root, root); } private bool IsMirror(TreeNode a, TreeNode b) { if (a == null && b == null) { return true; } if (a == null || b == null) { return false; } // 1. The two root nodes have the same value // 2. The left subtree of one root node is a mirror // reflection of the right subtree of the other root node // 3. The right subtree of one root node is a mirror // reflection of the left subtree of the other root node return a.val == b.val && IsMirror(a.left, b.right) && IsMirror(a.right, b.left); }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
true
false
C# || How To Traverse Bottom Up Binary Tree Level Order Using C#

The following is a module with functions which demonstrates how to traverse bottom up binary tree level order using C#.
1. Level Order Bottom – Problem Statement
Given the root of a binary tree, return the bottom-up level order traversal of its nodes’ values. (i.e., from left to right, level by level from leaf to root).
Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: [[15,7],[9,20],[3]]
Example 2:
Input: root = [1]
Output: [[1]]
Example 3:
Input: root = []
Output: []
2. Level Order Bottom – Solution
The following is a solution which demonstrates how to traverse bottom up binary tree level order.
The idea of this solution is to have a result list which keeps track of the items found on each level. A variable is also used to keep track of the maximum depth levels in the tree. The max depth level is used to insert node values into their appropriate result list slot.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253
// ============================================================================// Author: Kenneth Perkins// Date: Oct 20, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Determines how to traverse a tree bottom up level order// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { private List<IList<int>> result = new List<IList<int>>(); private int maxDepth = 0; public IList<IList<int>> LevelOrderBottom(TreeNode root) { Traverse(root, 0); return result; } private void Traverse(TreeNode node, int depth) { if (node == null) { return; } // Keep track of max depth level if (depth > maxDepth) { maxDepth = depth; } // Determine if new depth level should be added to the result list // Add the new level to the start of the result list if (result.Count == depth) { result.Insert(0, new List<int>()); } // Add the current node value to the corresponding result level index result[maxDepth - depth].Add(node.val); // Keep exploring left and right nodes Traverse(node.left, depth + 1); Traverse(node.right, depth + 1); }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[[15,7],[9,20],[3]]
[[1]]
[]
C# || How To Get The Sum Of Binary Tree Nodes With Even Valued Grandparents Using C#

The following is a module with functions which demonstrates how to get the sum of binary tree nodes with even valued grandparents using C#.
1. Sum Even Grandparent – Problem Statement
Given the root of a binary tree, return the sum of values of nodes with an even-valued grandparent. If there are no nodes with an even-valued grandparent, return 0.
A grandparent of a node is the parent of its parent if it exists.
Example 1:
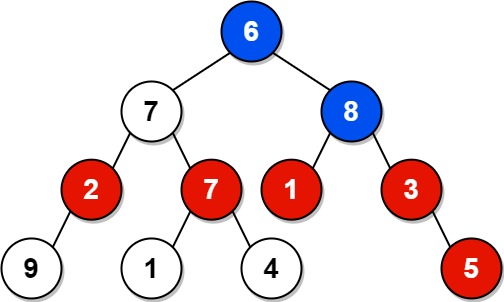
Input: root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
Output: 18
Explanation: The red nodes are the nodes with even-value grandparent while the blue nodes are the even-value grandparents.
Example 2:

Input: root = [1]
Output: 0
2. Sum Even Grandparent – Solution
The following is a solution which demonstrates how to get the sum of binary tree nodes with even valued grandparents.
The idea of this solution is to simply traverse the tree, and for each recursive call, we keep track of the parent node and the grandparent node of each node.
If a node has a grandparent, we check to see if it is an even number. If it is, the result is incremented.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
// ============================================================================// Author: Kenneth Perkins// Date: Oct 20, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Determines how to get the sum of even valued tree grandparents// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { private int result = 0; public int SumEvenGrandparent(TreeNode root) { Traverse(root, null, null); return result; } private void Traverse(TreeNode node, TreeNode parent, TreeNode grandParent) { if (node == null) { return; } // If a grandparent exists and its an even number, // add the current node value to the result if (grandParent != null && grandParent.val % 2 == 0) { result += node.val; } // Keep exploring left & right nodes // setting the current node as the parent // and the current parent node as the grandparent Traverse(node.left, node, parent); Traverse(node.right, node, parent); }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
18
0
C# || How To Get The Number Of Binary Tree Paths Equal To Path Sum Using C#

The following is a module with functions which demonstrates how to get the number of binary tree paths equal to path sum using C#.
1. Number Of Path Sum Paths – Problem Statement
Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.
The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).
Example 1:
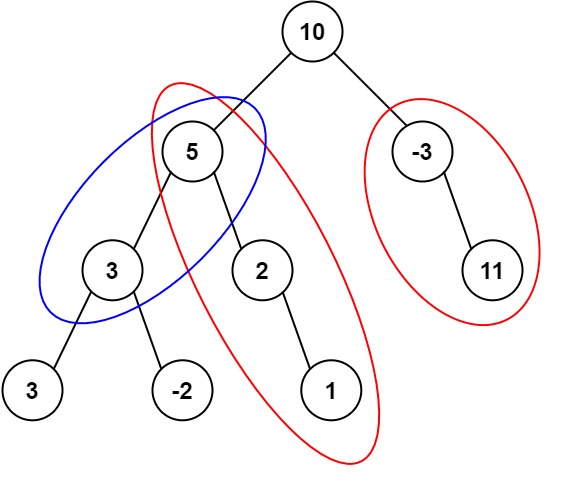
Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output: 3
Explanation: The paths that sum to 8 are shown.
Example 2:
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: 3
2. Number Of Path Sum Paths – Solution
The following is a solution which demonstrates how to get the number of binary tree paths equal to path sum.
The main idea here is that the sum at each level for each path is calculated. When the next level is explored, the value at the previous level is summed together with the node value at the current level.
A map dictionary is used to keep track of the sum at each level. If the prefix sum at the previous level is enough to equal the target path sum at the current level, the result count is incremented.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
// ============================================================================// Author: Kenneth Perkins// Date: Oct 18, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Determines how to get the number of tree paths equal to path sum// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { private int result = 0; private Dictionary<int, int> sumFrequency = new Dictionary<int, int>(); public int PathSum(TreeNode root, int targetSum) { sumFrequency[0] = 1; Search(root, targetSum, 0); return result; } public void Search(TreeNode node, int targetSum, int currentSum) { if (node == null) { return; } // Determine the current sum currentSum = currentSum + node.val; // Get the path prefix sum var prefixSum = currentSum - targetSum; if (sumFrequency.ContainsKey(prefixSum)) { result += sumFrequency[prefixSum]; } // Increment the number of times this prefix has been seen sumFrequency[currentSum] = (sumFrequency.ContainsKey(currentSum) ? sumFrequency[currentSum] : 0) + 1; // Keep exploring along branches finding the target sum Search(node.left, targetSum, currentSum); Search(node.right, targetSum, currentSum); // Remove value of this prefixSum (path's been explored) --sumFrequency[currentSum]; }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
3
3
C# || How To Get All Root To Leaf Binary Tree Paths Equal To Path Sum Using C#

The following is a module with functions which demonstrates how to get all the root to leaf binary tree paths equal to path sum using C#.
1. Root To Leaf Path Sum – Problem Statement
Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where the sum of the node values in the path equals targetSum. Each path should be returned as a list of the node values, not node references.
A root-to-leaf path is a path starting from the root and ending at any leaf node. A leaf is a node with no children.
Example 1:
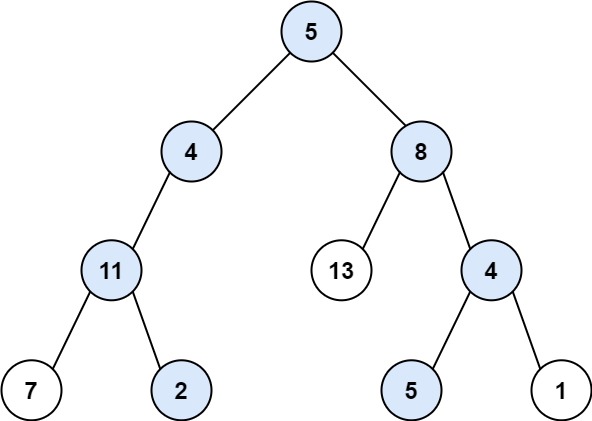
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2],[5,8,4,5]]
Explanation: There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
Example 2:
Input: root = [1,2,3], targetSum = 5
Output: []
Example 3:
Input: root = [1,2], targetSum = 0
Output: []
2. Root To Leaf Path Sum – Solution
The following is a solution which demonstrates how to get all the root to leaf binary tree paths equal to path sum.
The main idea here is that the sum at each level for each path is calculated until we reach the end of the root-to-leaf.
A list is used to store the node value at each level. When the next level is explored, the value is appended to the list, and the process continues.
When we reach the end of the leaf, we check to see if the target value has been reached. If so, we add the node values that make up the path to the result list.
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657
// ============================================================================// Author: Kenneth Perkins// Date: Oct 18, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Determines how to get all root to leaf path sum in a tree// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { private List<IList<int>> result = new List<IList<int>>(); public IList<IList<int>> PathSum(TreeNode root, int targetSum) { Search(root, targetSum, 0, new List<int>()); return result; } private void Search(TreeNode node, int targetSum, int currentSum, List<int> path) { if (node == null) { return; } // Add the node to this path path.Add(node.val); // Add the current value to the running total currentSum = currentSum + node.val; // Since this is a root-to-leaf check, evaluate for the // success condition when both left and right nodes are null if (node.left == null && node.right == null) { // Check to see if current value equals target if (currentSum == targetSum) { result.Add(new List<int>(path)); } } // Keep exploring along branches finding the target sum Search(node.left, targetSum, currentSum, path); Search(node.right, targetSum, currentSum, path); // Remove the last item added as this path has already been explored path.RemoveAt(path.Count - 1); }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[[5,4,11,2],[5,8,4,5]]
[]
[]
C# || How To Determine If Binary Tree Root To Leaf Path Sum Exists Using C#

The following is a module with functions which demonstrates how to determine if a binary tree root to leaf path sum exists using C#.
1. Has Path Sum – Problem Statement
Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.
A leaf is a node with no children.
Example 1:
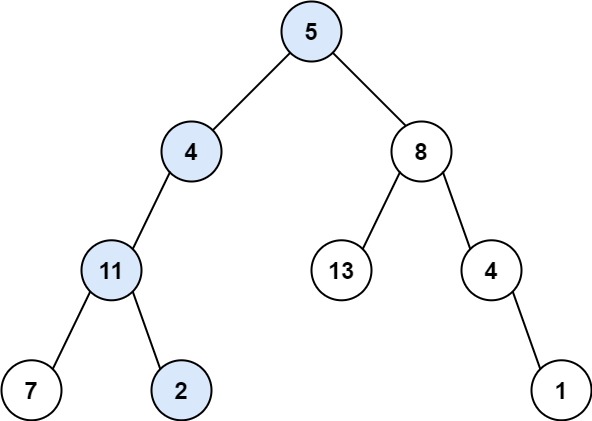
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
Example 2:

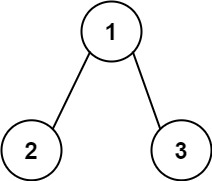
Input: root = [1,2,3], targetSum = 5
Output: false
Example 3:
Input: root = [1,2], targetSum = 0
Output: false
2. Has Path Sum – Solution
The following is a solution which demonstrates how to determine if a binary tree root to leaf path sum exists.
1234567891011121314151617181920212223242526272829303132333435363738394041424344
// ============================================================================// Author: Kenneth Perkins// Date: Oct 18, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Determines if a root to leaf path sum exists in a binary tree// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { public bool HasPathSum(TreeNode root, int targetSum) { return Search(root, targetSum); } public bool Search(TreeNode node, int targetSum) { if (node == null) { return false; } // Determine the current sum targetSum = targetSum - node.val; // Since this is a root-to-leaf check, evaluate for the // success condition when both left and right nodes are null if (node.left == null && node.right == null) { return targetSum == 0; } // Keep exploring along branches finding the target sum return Search(node.left, targetSum) || Search(node.right, targetSum); }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
true
false
false
C# || How To Convert Sorted Array To Binary Search Tree Using C#

The following is a module with functions which demonstrates how to convert a sorted array to a binary search tree using C#.
1. Sorted Array To BST – Problem Statement
Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.
A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.
Example 1:
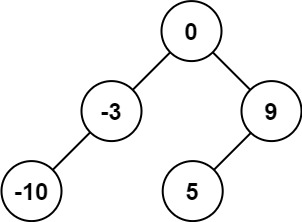
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted:

Example 2:
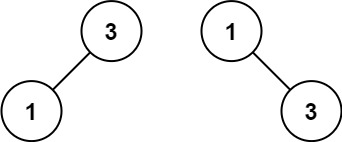
Input: nums = [1,3]
Output: [3,1]
Explanation: [1,3] and [3,1] are both a height-balanced BSTs.
2. Sorted Array To BST – Solution
The following is a solution which demonstrates how to convert a sorted array to a binary search tree.
12345678910111213141516171819202122232425262728293031323334353637
// ============================================================================// Author: Kenneth Perkins// Date: Oct 18, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Demonstrates how to convert sorted array to BST// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { public TreeNode SortedArrayToBST(int[] nums) { return BuildBST(nums, 0, nums.Length -1); } TreeNode BuildBST(int[] nums, int start, int end) { if (start > end) { return null; } var mid = start + (end - start) / 2; var node = new TreeNode(nums[mid]); node.left = BuildBST(nums, start, mid - 1); node.right = BuildBST(nums, mid + 1, end); return node; }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[0,-10,5,null,-3,null,9]
[1,null,3]
C# || How To Find Cousins In A Binary Tree Using C#

The following is a module with functions which demonstrates how to find the cousins in a binary tree using C#.
1. Is Cousins – Problem Statement
Given the root of a binary tree with unique values and the values of two different nodes of the tree x and y, return true if the nodes corresponding to the values x and y in the tree are cousins, or false otherwise.
Two nodes of a binary tree are cousins if they have the same depth with different parents.
Note that in a binary tree, the root node is at the depth 0, and children of each depth k node are at the depth k + 1.
Example 1:

Input: root = [1,2,3,4], x = 4, y = 3
Output: false
Example 2:

Input: root = [1,2,3,null,4,null,5], x = 5, y = 4
Output: true
Example 3:

Input: root = [1,2,3,null,4], x = 2, y = 3
Output: false
2. Is Cousins – Solution
The following is a solution which demonstrates how to determine if x and y values are cousins in a binary tree.
The idea here is to explore each path, finding the node values that represent x and y.
Once both values are found, save the depth and parent node, and determine if they are cousins
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061
// ============================================================================// Author: Kenneth Perkins// Date: Oct 17, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Determines if x and y are cousins in a binary tree// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { // For the x parent and depth values private int xParent = -1; private int xDepth = -1; // For the y parent and depth values private int yParent = -1; private int yDepth = -1; public bool IsCousins(TreeNode root, int x, int y) { Search(root, x, y, root.val, 0); // Check for success condition return xParent != yParent && xDepth == yDepth; } private void Search(TreeNode node, int x, int y, int parent, int depth) { // Values have been found if (xParent != -1 && yParent != -1) { return; } if (node == null) { return; } if (node.val == x) { // Set the x parent and depth values xParent = parent; xDepth = depth; } else if (node.val == y) { // Set the y parent and depth values yParent = parent; yDepth = depth; } else { // Keep exploring along branches for the success condition Search(node.left, x, y, node.val, depth + 1); Search(node.right, x, y, node.val, depth + 1); } }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
false
true
false
C# || How To Construct A Binary Search Tree From Preorder Traversal Using C#

The following is a module with functions which demonstrates how to construct a binary search tree from preorder traversal using C#.
1. Binary Tree From Preorder – Problem Statement
Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.
It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.
A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.
A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.
Example 1:
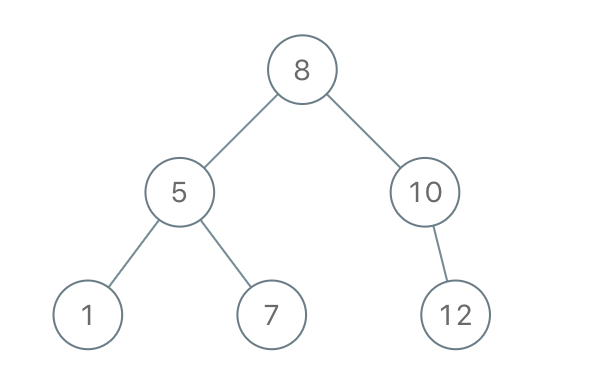
Input: preorder = [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]
Example 2:
Input: preorder = [1,3]
Output: [1,null,3]
2. Binary Tree From Preorder – Solution
The following is a solution which demonstrates how to construct a binary search tree from preorder traversal.
123456789101112131415161718192021222324252627282930313233343536373839
// ============================================================================// Author: Kenneth Perkins// Date: Oct 16, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Demonstrates how to construct a BST from preorder traversal// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { private int currentIndex = 0; public TreeNode BstFromPreorder(int[] preorder) { return BuildBST(preorder, int.MaxValue); } TreeNode BuildBST(int[] preorder, int parentValue) { if (currentIndex == preorder.Length || preorder[currentIndex] > parentValue) { return null; } var currentValue = preorder[currentIndex++]; var node = new TreeNode(currentValue); node.left = BuildBST(preorder, currentValue); node.right = BuildBST(preorder, parentValue); return node; }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[8,5,10,1,7,null,12]
[1,null,3]
C# || How To Traverse A Binary Tree Postorder Using C#

The following is a module with functions which demonstrates how to traverse a binary tree post order using C#.
1. Binary Tree Traversal – Problem Statement
Given the root of a binary tree, return the postorder traversal of its nodes’ values.
Example 1:

Input: root = [1,null,2,3]
Output: [3,2,1]
Example 2:
Input: root = []
Output: []
Example 3:
Input: root = [1]
Output: [1]
Example 4:
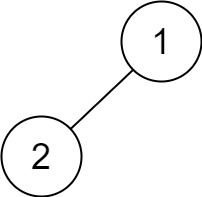
Input: root = [1,2]
Output: [2,1]
Example 5:
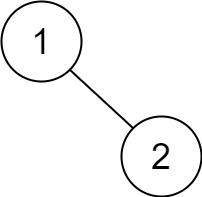
Input: root = [1,null,2]
Output: [2,1]
2. Binary Tree Traversal – Solution
The following is a solution which demonstrates how to traverse a binary tree post order.
12345678910111213141516171819202122232425262728293031323334353637383940
// ============================================================================// Author: Kenneth Perkins// Date: Oct 13, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Demonstrates how to traverse a binary tree post order// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { private List<int> result = new List<int>(); public IList<int> PostorderTraversal(TreeNode root) { Traverse(root); return result; } public void Traverse(TreeNode node) { if (node == null) { return; } Traverse(node.left); Traverse(node.right); result.Add(node.val); } }// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[3,2,1]
[]
[1]
[2,1]
[2,1]
C# || How To Traverse A Binary Tree Preorder Using C#

The following is a module with functions which demonstrates how to traverse a binary tree pre order using C#.
1. Binary Tree Traversal – Problem Statement
Given the root of a binary tree, return the preorder traversal of its nodes’ values.
Example 1:
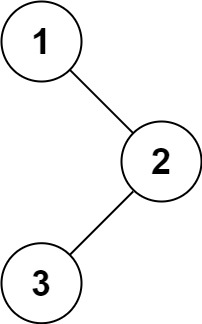
Input: root = [1,null,2,3]
Output: [1,2,3]
Example 2:
Input: root = []
Output: []
Example 3:
Input: root = [1]
Output: [1]
Example 4:

Input: root = [1,2]
Output: [1,2]
Example 5:

Input: root = [1,null,2]
Output: [1,2]
2. Binary Tree Traversal – Solution
The following is a solution which demonstrates how to traverse a binary tree pre order.
12345678910111213141516171819202122232425262728293031323334353637383940
// ============================================================================// Author: Kenneth Perkins// Date: Oct 13, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Demonstrates how to traverse a binary tree pre order// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { private List<int> result = new List<int>(); public IList<int> PreorderTraversal(TreeNode root) { Traverse(root); return result; } public void Traverse(TreeNode node) { if (node == null) { return; } result.Add(node.val); Traverse(node.left); Traverse(node.right); }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[1,2,3]
[]
[1]
[1,2]
[1,2]
C# || How To Traverse A Binary Tree Inorder Using C#

The following is a module with functions which demonstrates how to traverse a binary tree in order using C#.
1. Binary Tree Traversal – Problem Statement
Given the root of a binary tree, return the inorder traversal of its nodes’ values.
Example 1:

Input: root = [1,null,2,3]
Output: [1,3,2]
Example 2:
Input: root = []
Output: []
Example 3:
Input: root = [1]
Output: [1]
Example 4:

Input: root = [1,2]
Output: [2,1]
Example 5:

Input: root = [1,null,2]
Output: [1,2]
2. Binary Tree Traversal – Solution
The following is a solution which demonstrates how to traverse a binary tree in order.
12345678910111213141516171819202122232425262728293031323334353637383940
// ============================================================================// Author: Kenneth Perkins// Date: Oct 13, 2021// Taken From: http://programmingnotes.org/// File: Solution.cs// Description: Demonstrates how to traverse a binary tree in order// ============================================================================/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */public class Solution { private List<int> result = new List<int>(); public IList<int> InorderTraversal(TreeNode root) { Traverse(root); return result; } public void Traverse(TreeNode node) { if (node == null) { return; } Traverse(node.left); result.Add(node.val); Traverse(node.right); }}// http://programmingnotes.org/
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[1,3,2]
[]
[1]
[2,1]
[1,2]












