Tag Archives: breadth first search
C# || How To Get Smallest String Starting From Leaf Using C#

The following is a module with functions which demonstrates how to get smallest string starting from leaf using C#.
1. Smallest String Starting From Leaf – Problem Statement
You are given the root of a binary tree where each node has a value in the range [0, 25] representing the letters 'a' to 'z'.
Return the lexicographically smallest string that starts at a leaf of this tree and ends at the root.
As a reminder, any shorter prefix of a string is lexicographically smaller.
- For example,
"ab"is lexicographically smaller than"aba".
A leaf of a node is a node that has no children.
Example 1:
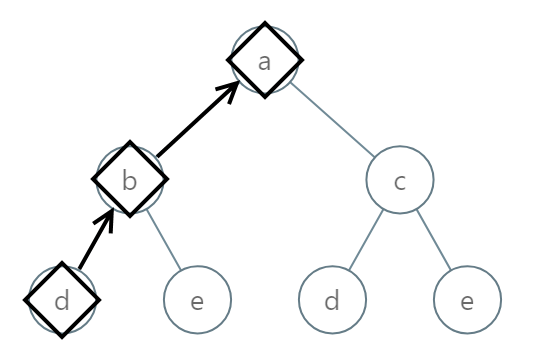
Input: root = [0,1,2,3,4,3,4]
Output: "dba"
Example 2:
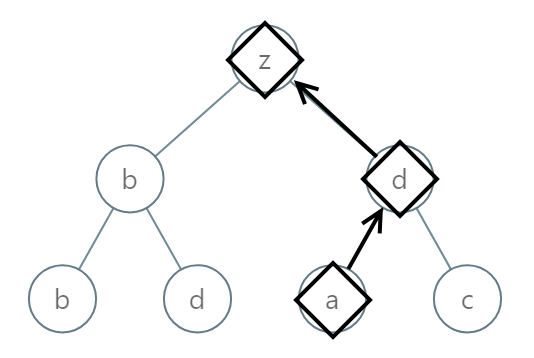
Input: root = [25,1,3,1,3,0,2]
Output: "adz"
Example 3:
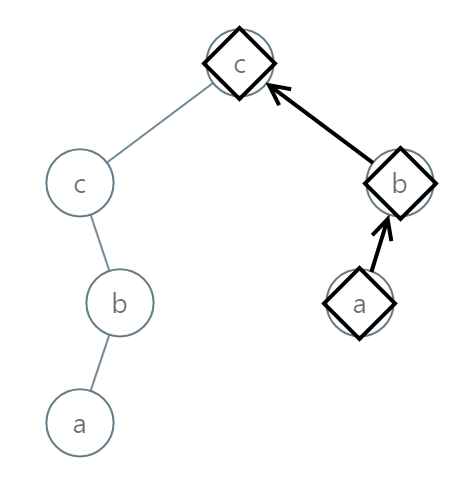
Input: root = [2,2,1,null,1,0,null,0]
Output: "abc"
2. Smallest String Starting From Leaf – Solution
The following is a solution which demonstrates how to convert get smallest string starting from leaf.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
// ============================================================================ // Author: Kenneth Perkins // Date: Dec 1, 2024 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to get smallest string starting from leaf // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { public string SmallestFromLeaf(TreeNode root) { var smallestString = ""; var queue = new Queue<KeyValuePair<TreeNode, string>>(); // Enqueue root node to queue along with its value converted to a character queue.Enqueue(new KeyValuePair<TreeNode, string>(root, ((char)(root.val + 'a')).ToString())); // Perform BFS traversal until queue is empty while (queue.Count > 0) { // Pop the leftmost node and its corresponding string from queue var pair = queue.Dequeue(); var node = pair.Key; var currentString = pair.Value; // If current node is a leaf node if (node.left == null && node.right == null) { // Update smallest_string if it's empty or current string is smaller if (string.IsNullOrEmpty(smallestString)) { smallestString = currentString; } else { smallestString = currentString.CompareTo(smallestString) < 0 ? currentString : smallestString; } } // If current node has a left child, append it to queue if (node.left != null) { queue.Enqueue(new KeyValuePair<TreeNode, string>(node.left, (char)(node.left.val + 'a') + currentString)); } // If current node has a right child, append it to queue if (node.right != null) { queue.Enqueue(new KeyValuePair<TreeNode, string>(node.right, (char)(node.right.val + 'a') + currentString)); } } return smallestString; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
"dba"
"adz"
"abc"
C# || How To Determine If A Binary Tree Is Even Odd Tree Using C#

The following is a module with functions which demonstrates how to determine if a binary tree is an even odd tree using C#.
1. Is Even Odd Tree – Problem Statement
A binary tree is named Even-Odd if it meets the following conditions:
- The root of the binary tree is at level index 0, its children are at level index 1, their children are at level index 2, etc.
- For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
- For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).
Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.
Example 1:
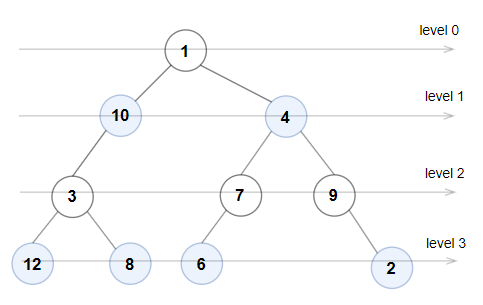
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
Output: true
Explanation: The node values on each level are:
Level 0: [1]
Level 1: [10,4]
Level 2: [3,7,9]
Level 3: [12,8,6,2]
Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.
Example 2:
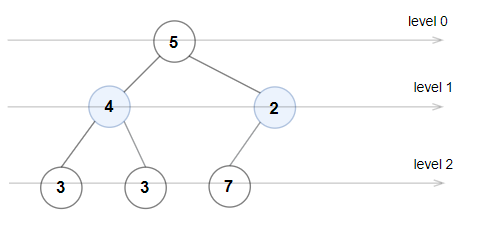
Input: root = [5,4,2,3,3,7]
Output: false
Explanation: The node values on each level are:
Level 0: [5]
Level 1: [4,2]
Level 2: [3,3,7]
Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.
Example 3:
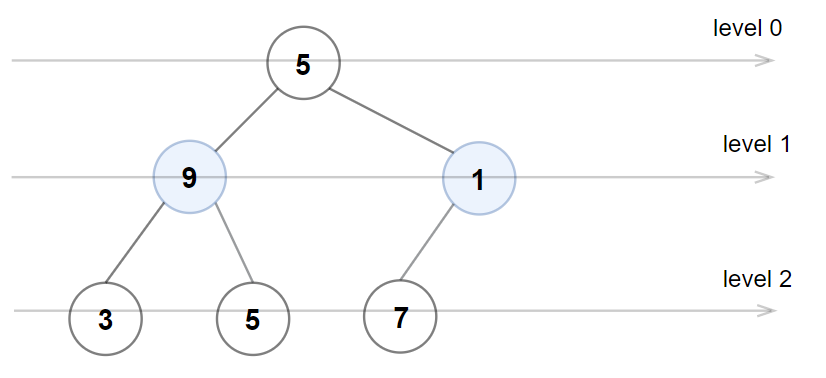
Input: root = [5,9,1,3,5,7]
Output: false
Explanation: Node values in the level 1 should be even integers.
2. Is Even Odd Tree – Solution
The following is a solution which demonstrates how to determine if a binary tree is an even odd tree.
This solution uses breadth-first search.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
// ============================================================================ // Author: Kenneth Perkins // Date: Mar 1, 2024 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to determine an even odd tree // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { public bool IsEvenOddTree(TreeNode root) { var queue = new Queue<TreeNode>(); queue.Enqueue(root); var isEvenLevel = true; while (queue.Count > 0) { int previousValue = isEvenLevel ? int.MinValue : int.MaxValue; for (var size = queue.Count - 1; size >= 0; --size) { var currentNode = queue.Dequeue(); if (isEvenLevel) { if (IsEven(currentNode.val) || previousValue >= currentNode.val) { return false; } } else { if (!IsEven(currentNode.val) || previousValue <= currentNode.val) { return false; } } if (currentNode.left != null) { queue.Enqueue(currentNode.left); } if (currentNode.right != null) { queue.Enqueue(currentNode.right); } previousValue = currentNode.val; } isEvenLevel = !isEvenLevel; } return true; } private bool IsEven(int value) { return value % 2 == 0; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
true
false
false
C# || Parallel Courses III – How To Find Minimum Number Months To Complete All Courses Using C#

The following is a module with functions which demonstrates how to find the minimum number of months needed to complete all courses using C#.
1. Minimum Time – Problem Statement
You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given a 2D integer array relations where relations[j] = [prevCoursej, nextCoursej] denotes that course prevCoursej has to be completed before course nextCoursej (prerequisite relationship). Furthermore, you are given a 0-indexed integer array time where time[i] denotes how many months it takes to complete the (i+1)th course.
You must find the minimum number of months needed to complete all the courses following these rules:
- You may start taking a course at any time if the prerequisites are met.
- Any number of courses can be taken at the same time.
Return the minimum number of months needed to complete all the courses.
Note: The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
Example 1:

Input: n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
Output: 8
Explanation: The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
Example 2:
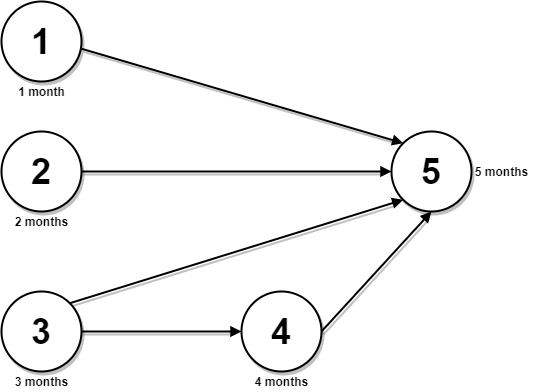
Input: n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
Output: 12
Explanation: The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
2. Minimum Time – Solution
The following is a solution which demonstrates how to find the minimum number of months needed to complete all courses.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
// ============================================================================ // Author: Kenneth Perkins // Date: Nov 1, 2023 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to find the minimum months complete courses // ============================================================================ public class Solution { public int MinimumTime(int n, int[][] relations, int[] time) { var graph = new Dictionary<int, List<int>>(); for (int i = 0; i < n; i++) { graph[i] = new List<int>(); } int[] indegree = new int[n]; foreach (int[] edge in relations) { int x = edge[0] - 1; int y = edge[1] - 1; graph[x].Add(y); indegree[y]++; } var queue = new Queue<int>(); int[] maxTime = new int[n]; for (int node = 0; node < n; node++) { if (indegree[node] == 0) { queue.Enqueue(node); maxTime[node] = time[node]; } } while (queue.Count > 0) { int node = queue.Dequeue(); foreach (int neighbor in graph[node]) { maxTime[neighbor] = Math.Max(maxTime[neighbor], maxTime[node] + time[neighbor]); indegree[neighbor]--; if (indegree[neighbor] == 0) { queue.Enqueue(neighbor); } } } int ans = 0; for (int node = 0; node < n; node++) { ans = Math.Max(ans, maxTime[node]); } return ans; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
8
12
C# || How To Find Largest Value In Each Binary Tree Row Using C#

The following is a module with functions which demonstrates how to find the largest value in each binary tree row using C#.
1. Largest Values – Problem Statement
Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).
Example 1:
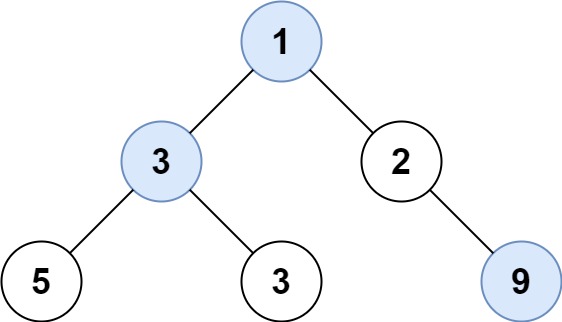
Input: root = [1,3,2,5,3,null,9]
Output: [1,3,9]
Example 2:
Input: root = [1,2,3]
Output: [1,3]
2. Largest Values – Solution
The following is a solution which demonstrates how to find the largest value in each binary tree row.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 28, 2023 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to find the largest value binary tree row // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { public IList<int> LargestValues(TreeNode root) { if (root == null) { return new List<int>(); } var ans = new List<int>(); var queue = new Queue<TreeNode>(); queue.Enqueue(root); while (queue.Count > 0) { int currMax = int.MinValue; for (int i = queue.Count -1; i >= 0; --i) { var node = queue.Dequeue(); currMax = Math.Max(currMax, node.val); if (node.left != null) { queue.Enqueue(node.left); } if (node.right != null) { queue.Enqueue(node.right); } } ans.Add(currMax); } return ans; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[1,3,9]
[1,3]
C# || How To Find The Minimum Fuel Cost To Report To The Capital Using C#

The following is a module with functions which demonstrates how to find the minimum fuel cost to report to the capital using C#.
1. Minimum Fuel Cost – Problem Statement
There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of n cities numbered from 0 to n – 1 and exactly n – 1 roads. The capital city is city 0. You are given a 2D integer array roads where roads[i] = [ai, bi] denotes that there exists a bidirectional road connecting cities ai and bi.
There is a meeting for the representatives of each city. The meeting is in the capital city.
There is a car in each city. You are given an integer seats that indicates the number of seats in each car.
A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel.
Return the minimum number of liters of fuel to reach the capital city.
Example 1:
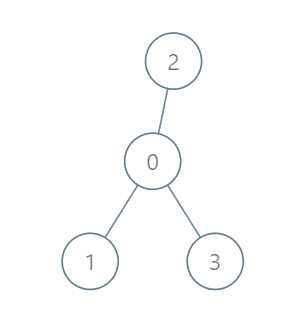
Input: roads = [[0,1],[0,2],[0,3]], seats = 5
Output: 3
Explanation:
- Representative1 goes directly to the capital with 1 liter of fuel.
- Representative2 goes directly to the capital with 1 liter of fuel.
- Representative3 goes directly to the capital with 1 liter of fuel.
It costs 3 liters of fuel at minimum.
It can be proven that 3 is the minimum number of liters of fuel needed.
Example 2:
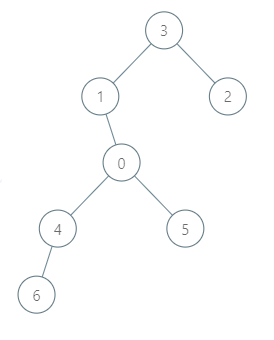
Input: roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
Output: 7
Explanation:
- Representative2 goes directly to city 3 with 1 liter of fuel.
- Representative2 and representative3 go together to city 1 with 1 liter of fuel.
- Representative2 and representative3 go together to the capital with 1 liter of fuel.
- Representative1 goes directly to the capital with 1 liter of fuel.
- Representative5 goes directly to the capital with 1 liter of fuel.
- Representative6 goes directly to city 4 with 1 liter of fuel.
- Representative4 and representative6 go together to the capital with 1 liter of fuel.
It costs 7 liters of fuel at minimum.
It can be proven that 7 is the minimum number of liters of fuel needed.
Example 3:

Input: roads = [], seats = 1
Output: 0
Explanation: No representatives need to travel to the capital city.
2. Minimum Fuel Cost – Solution
The following is a solution which demonstrates how to find the minimum fuel cost to report to the capital.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
// ============================================================================ // Author: Kenneth Perkins // Date: May 24, 2023 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to find minimum fuel cost to the capital // ============================================================================ public class Solution { public long MinimumFuelCost(int[][] roads, int seats) { int n = roads.Length + 1; var adj = new Dictionary<int, List<int>>(); int[] degree = new int[n]; foreach (int[] road in roads) { if (!adj.ContainsKey(road[0])) { adj[road[0]] = new List<int>(); } adj[road[0]].Add(road[1]); if (!adj.ContainsKey(road[1])) { adj[road[1]] = new List<int>(); } adj[road[1]].Add(road[0]); ++degree[road[0]]; ++degree[road[1]]; } return BFS(n, adj, degree, seats); } public long BFS(int n, Dictionary<int, List<int>> adj, int[] degree, int seats) { var q = new Queue<int>(); for (int i = 1; i < n; i++) { if (degree[i] == 1) { q.Enqueue(i); } } int[] representatives = new int[n]; Array.Fill(representatives, 1); long fuel = 0; while (q.Count > 0) { int node = q.Dequeue(); fuel += (long)Math.Ceiling((double) representatives[node] / seats); foreach (int neighbor in adj[node]) { --degree[neighbor]; representatives[neighbor] += representatives[node]; if (degree[neighbor] == 1 && neighbor != 0) { q.Enqueue(neighbor); } } } return fuel; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
3
7
0
C# || How To Find The Nearest Exit From Entrance In Maze Using C#

The following is a module with functions which demonstrates how to find the nearest exit from the entrance in a maze using C#.
1. Nearest Exit – Problem Statement
You are given an m x n matrix maze (0-indexed) with empty cells (represented as ‘.’) and walls (represented as ‘+’). You are also given the entrance of the maze, where entrance = [entrancerow, entrancecol] denotes the row and column of the cell you are initially standing at.
In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrance does not count as an exit.
Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.
Example 1:
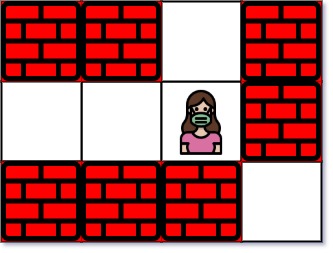
Input: maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
Output: 1
Explanation: There are 3 exits in this maze at [1,0], [0,2], and [2,3].
Initially, you are at the entrance cell [1,2].
- You can reach [1,0] by moving 2 steps left.
- You can reach [0,2] by moving 1 step up.
It is impossible to reach [2,3] from the entrance.
Thus, the nearest exit is [0,2], which is 1 step away.
Example 2:

Input: maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
Output: 2
Explanation: There is 1 exit in this maze at [1,2].
[1,0] does not count as an exit since it is the entrance cell.
Initially, you are at the entrance cell [1,0].
- You can reach [1,2] by moving 2 steps right.
Thus, the nearest exit is [1,2], which is 2 steps away.
Example 3:

Input: maze = [[".","+"]], entrance = [0,0]
Output: -1
Explanation: There are no exits in this maze.
2. Nearest Exit – Solution
The following is a solution which demonstrates how find the nearest exit from the entrance in a maze.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
// ============================================================================ // Author: Kenneth Perkins // Date: Dec 1, 2022 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to find nearest exit from entrance in maze // ============================================================================ public class Solution { public int NearestExit(char[][] maze, int[] entrance) { int rows = maze.Length; int cols = maze[0].Length; var directions = new List<KeyValuePair<int, int>>() { // Direction coordinates: (y, x) new KeyValuePair<int, int>(1, 0), new KeyValuePair<int, int>(-1, 0), new KeyValuePair<int, int>(0, 1), new KeyValuePair<int, int>(0, -1) }; char VISITED = '+'; char NOT_VISITED = '.'; // Mark the entrance as visited since its not a exit. int startRow = entrance[0]; int startCol = entrance[1]; maze[startRow][startCol] = VISITED; // Start BFS from the entrance, and use a queue `queue` to store all // the cells to be visited. var queue = new Queue<int[]>(); queue.Enqueue(new int[]{startRow, startCol, 0}); while (queue.Count > 0) { int[] currState = queue.Dequeue(); int currRow = currState[0]; int currCol = currState[1]; int currDistance = currState[2]; // For the current cell, check its four neighbor cells. foreach (var dir in directions) { int nextRow = currRow + dir.Key; int nextCol = currCol + dir.Value; // If there exists an unvisited empty neighbor: if (IsValidCell(maze, nextRow, nextCol) && maze[nextRow][nextCol] == NOT_VISITED) { // If this empty cell is an exit, return distance + 1. if (nextRow == 0 || nextRow == rows - 1 || nextCol == 0 || nextCol == cols - 1) { return currDistance + 1; } // Otherwise, add this cell to 'queue' and mark it as visited. maze[nextRow][nextCol] = VISITED; queue.Enqueue(new int[]{nextRow, nextCol, currDistance + 1}); } } } // If we finish iterating without finding an exit, return -1. return -1; } private bool IsValidCell(char[][] grid, int row, int col) { return row >= 0 && row < grid.Length && col >= 0 && col < grid[row].Length; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
1
2
-1
C# || Two Sum IV – How To Get Two Numbers In Binary Search Tree Equal To Target Value Using C#

The following is a module with functions which demonstrates how to get two numbers in a binary search tree equal to target value using C#.
1. Find Target – Problem Statement
Given the root of a Binary Search Tree and a target number k, return true if there exist two elements in the BST such that their sum is equal to the given target.
Example 1:

Input: root = [5,3,6,2,4,null,7], k = 9
Output: true
Example 2:

Input: root = [5,3,6,2,4,null,7], k = 28
Output: false
2. Find Target – Solution
The following are two solutions which demonstrates how to get two numbers in a binary search tree equal to target value.
Both solutions use a set to keep track of the items already seen.
Each time a new node is encountered, we subtract the target value from the current node value. If the difference amount from subtracting the two numbers exists in the set, a 2 sum combination exists in the tree
1. Recursive
The following solution uses Depth First Search when looking for the target value.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 9, 2022 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to get two numbers equal to target value // ============================================================================ public class Solution { public bool FindTarget(TreeNode root, int k) { return Traverse(root, k, new HashSet<int>()); } private bool Traverse(TreeNode node, int k, HashSet<int> seen) { if (node == null) { return false; } // Get remaining value var remaining = k - node.val; // Check if remaining value has been seen if (seen.Contains(remaining)) { return true; } // Add current node value to items seen seen.Add(node.val); // Keep traversing left and right looking for 2 sum return Traverse(node.left, k, seen) || Traverse(node.right, k, seen); } }// http://programmingnotes.org/ |
2. Iterative
The following solution uses Breadth First Search when looking for the target value.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 9, 2022 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to get two numbers equal to target value // ============================================================================ public class Solution { public bool FindTarget(TreeNode root, int k) { if (root == null) { return false; } // Declare stack var stack = new Stack<TreeNode>(); // Keep track of values seen var seen = new HashSet<int>(); // Add root to stack stack.Push(root); // Loop through items on the stack while (stack.Count > 0) { // Get current node var node = stack.Pop(); // Get remaining value var remaining = k - node.val; // Check if remaining value has been seen if (seen.Contains(remaining)) { return true; } else { // Keep traversing left and right looking for 2 sum if (node.left != null) { stack.Push(node.left); } if (node.right != null) { stack.Push(node.right); } } // Add current node value to items seen seen.Add(node.val); } return false; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
true
false
C# || How To Find The Shortest Clear Path In A Binary Matrix Using C#

The following is a module with functions which demonstrates how to find the shortest clear path in a binary matrix using C#.
1. Shortest Path Binary Matrix – Problem Statement
Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.
A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n – 1, n – 1)) such that:
- All the visited cells of the path are 0.
- All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).
The length of a clear path is the number of visited cells of this path.
Example 1:
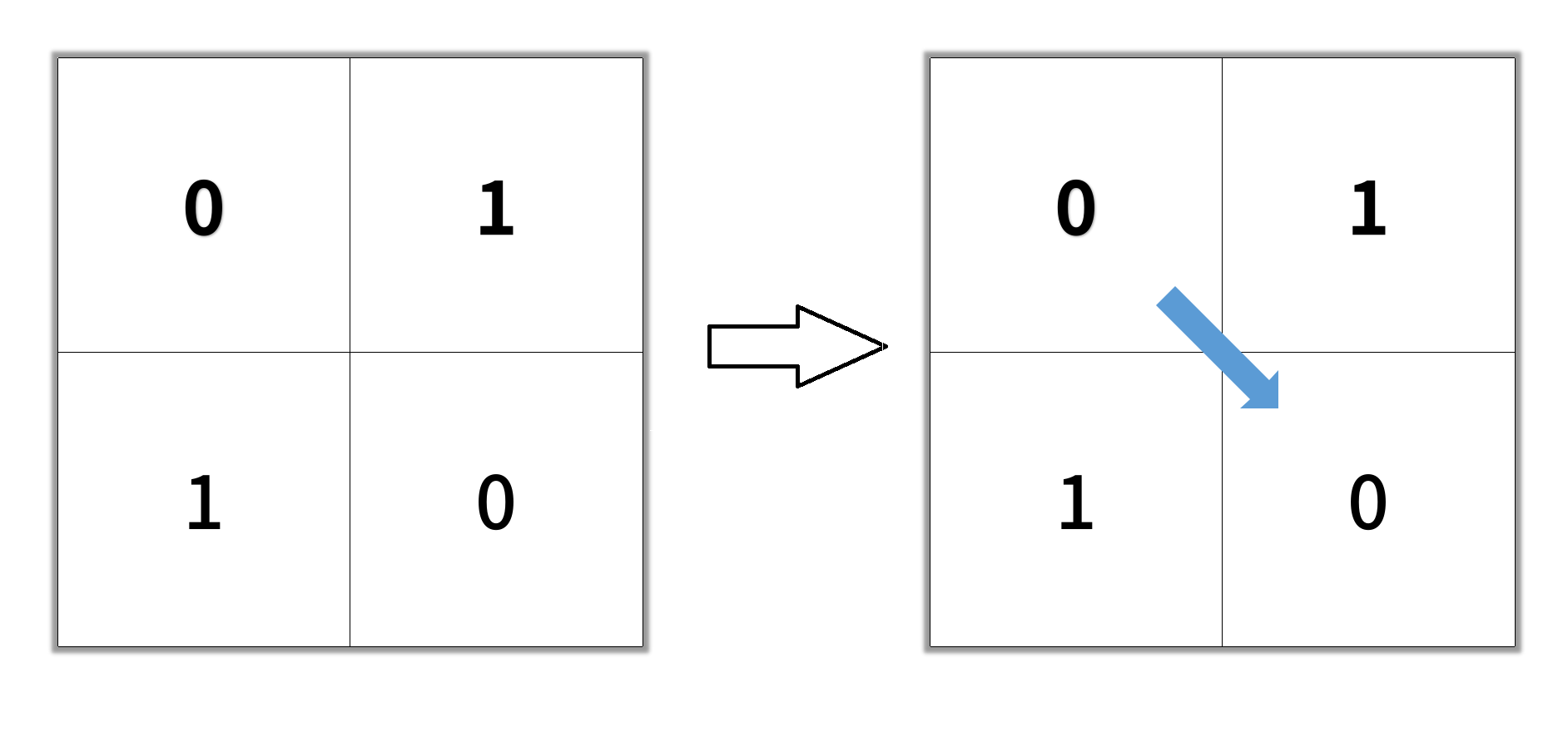
Input: grid = [[0,1],[1,0]]
Output: 2
Example 2:
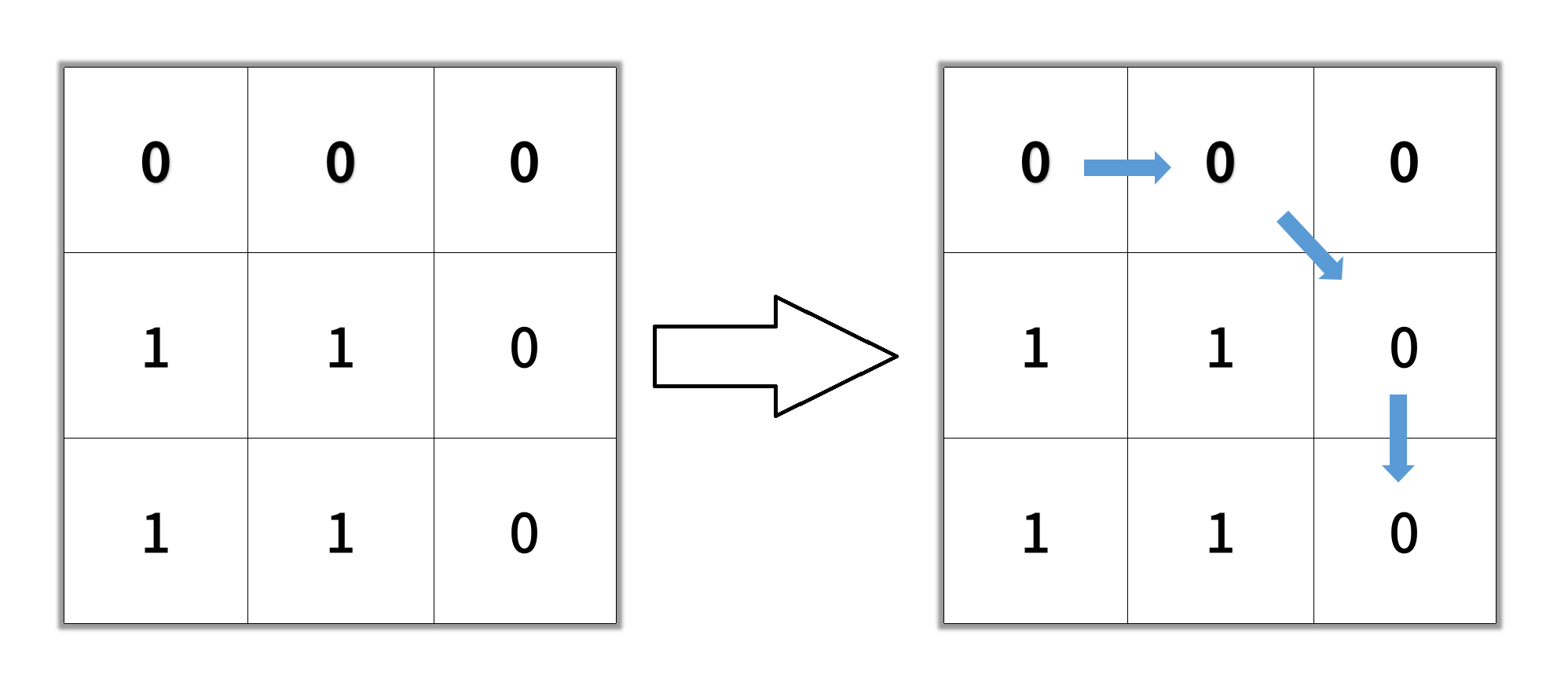
Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4
Example 3:
Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1
2. Shortest Path Binary Matrix – Solution
The following is a solution which demonstrates how find the shortest clear path in a binary matrix.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
// ============================================================================ // Author: Kenneth Perkins // Date: Jun 3, 2022 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to find shortest path binary matrix // ============================================================================ public class Solution { // Search directions List<KeyValuePair<int, int>> directions = new List<KeyValuePair<int, int>>() { // Direction coordinates: (y, x) new KeyValuePair<int, int>(0, -1), new KeyValuePair<int, int>(0, 1), new KeyValuePair<int, int>(-1, 0), new KeyValuePair<int, int>(1, 0), new KeyValuePair<int, int>(1, 1), new KeyValuePair<int, int>(-1, -1), new KeyValuePair<int, int>(-1, 1), new KeyValuePair<int, int>(1, -1) }; public int ShortestPathBinaryMatrix(int[][] grid) { var NOT_VISITED = 0; var VISITED = 1; if (grid[0][0] == VISITED) { return -1; } var queue = new Queue<KeyValuePair<int, int>>(); queue.Enqueue(new KeyValuePair<int, int>(0, 0)); grid[0][0] = VISITED; var result = 0; while(queue.Count > 0) { ++result; for (var itemCount = queue.Count; itemCount > 0; --itemCount) { var current = queue.Dequeue(); // Get the current coordinates var row = current.Key; var col = current.Value; if (row == grid.Length - 1 && col == grid[row].Length - 1) { return result; } // Search in different directions foreach (var direction in directions) { var newRow = row + direction.Key; var newCol = col + direction.Value; if (IsValidCell(grid, newRow, newCol) && grid[newRow][newCol] == NOT_VISITED) { grid[newRow][newCol] = VISITED; queue.Enqueue(new KeyValuePair<int, int>(newRow, newCol)); } } } } return -1; } private bool IsValidCell(int[][] grid, int row, int col) { return row >= 0 && row < grid.Length && col >= 0 && col < grid[row].Length; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
2
4
-1
C# || Jump Game III – How To Check If You Can Reach Target Value In Array Using C#

The following is a module with functions which demonstrates how to check if you can reach a target value in an array using C#.
1. Can Reach – Problem Statement
Given an array of non-negative integers arr, you are initially positioned at start index of the array. When you are at index i, you can jump to i + arr[i] or i – arr[i], check if you can reach to any index with value 0.
Notice that you can not jump outside of the array at any time.
Example 1:
Input: arr = [4,2,3,0,3,1,2], start = 5
Output: true
Explanation:
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3
Example 2:
Input: arr = [4,2,3,0,3,1,2], start = 0
Output: true
Explanation:
One possible way to reach at index 3 with value 0 is:
index 0 -> index 4 -> index 1 -> index 3
Example 3:
Input: arr = [3,0,2,1,2], start = 2
Output: false
Explanation: There is no way to reach at index 1 with value 0.
2. Can Reach – Solution
The following are two solutions which demonstrates how to check if you can reach a target value in an array.
The following solution uses Depth First Search when looking for the target value.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
// ============================================================================ // Author: Kenneth Perkins // Date: Dec 8, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Determines if a target value can be reached in an array // ============================================================================ public class Solution { public bool CanReach(int[] arr, int start) { var visited = new bool[arr.Length]; return DFS(arr, start, visited); } public bool DFS(int[] arr, int currentIndex, bool[] visited) { // Make sure parameters are in bounds if (currentIndex < 0 || currentIndex >= arr.Length) { return false; } // Check to see if the index has been visited if (visited[currentIndex]) { return false; } // Check to see if we found the target value if (arr[currentIndex] == 0) { return true; } // Mark current index as visited visited[currentIndex] = true; // Keep searching forwards and backwards var forwards = currentIndex + arr[currentIndex]; var backwards = currentIndex - arr[currentIndex]; return DFS(arr, backwards, visited) || DFS(arr, forwards, visited); } }// http://programmingnotes.org/ |
The following solution uses Breadth First Search when looking for the target value.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
// ============================================================================ // Author: Kenneth Perkins // Date: Dec 8, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Determines if a target value can be reached in an array // ============================================================================ public class Solution { public bool CanReach(int[] arr, int start) { var visited = new bool[arr.Length]; var queue = new Queue<int>(); queue.Enqueue(start); while (queue.Count > 0) { var currentIndex = queue.Dequeue(); // Check to see if we found the target value if (arr[currentIndex] == 0) { return true; } // Mark current index as visited visited[currentIndex] = true; // Keep searching forwards and backwards var forwards = currentIndex + arr[currentIndex]; var backwards = currentIndex - arr[currentIndex]; var directions = new List<int>{forwards, backwards}; foreach (var direction in directions) { if (direction >= 0 && direction < arr.Length && !visited[direction]) { queue.Enqueue(direction); } } } return false; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
true
true
false
C# || How To Find All Paths From Source To Target In Graph Using C#

The following is a module with functions which demonstrates how to find all paths from source to target in a graph using C#.
1. All Paths Source Target – Problem Statement
Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n – 1, find all possible paths from node 0 to node n – 1 and return them in any order.
The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).
Example 1:

Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
Example 2:

Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
Example 3:
Input: graph = [[1],[]]
Output: [[0,1]]
Example 4:
Input: graph = [[1,2,3],[2],[3],[]]
Output: [[0,1,2,3],[0,2,3],[0,3]]
Example 5:
Input: graph = [[1,3],[2],[3],[]]
Output: [[0,1,2,3],[0,3]]
2. All Paths Source Target – Solution
The following is a solution which demonstrates how to find all paths from source to target in a graph.
This solution uses Breadth First Search and backtracking when looking for paths.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
// ============================================================================ // Author: Kenneth Perkins // Date: Nov 28, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to find all paths in a graph // ============================================================================ public class Solution { public IList<IList<int>> AllPathsSourceTarget(int[][] graph) { var result = new List<IList<int>>(); var queue = new Queue<List<int>>(); queue.Enqueue(new List<int>{0}); while (queue.Count > 0) { var currentPath = queue.Dequeue(); var currentNode = currentPath[currentPath.Count - 1]; if (currentNode == graph.Length - 1) { result.Add(currentPath); } else { foreach (var child in graph[currentNode]) { currentPath.Add(child); queue.Enqueue(new List<int>(currentPath)); currentPath.RemoveAt(currentPath.Count - 1); } } } return result; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[[0,1,3],[0,2,3]]
[[0,4],[0,3,4],[0,1,4],[0,1,3,4],[0,1,2,3,4]]
[[0,1]]
[[0,3],[0,2,3],[0,1,2,3]]
[[0,3],[0,1,2,3]]
C# || How To Capture All Surrounded Regions ‘X’ & ‘O’ In Board Matrix Using C#

The following is a module with functions which demonstrates how to capture all surrounded regions ‘X’ and ‘O’ in a board matrix using C#.
1. Surrounded Regions – Problem Statement
Given an m x n matrix board containing ‘X’ and ‘O’, capture all regions that are 4-directionally surrounded by ‘X’.
A region is captured by flipping all ‘O’s into ‘X’s in that surrounded region.
Example 1:

Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
Explanation: Surrounded regions should not be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.
Example 2:
Input: board = [["X"]]
Output: [["X"]]
2. Surrounded Regions – Solution
The following is a solution which demonstrates how to capture all surrounded regions ‘X’ and ‘O’ in a board matrix.
This solution uses Breadth First Search when looking for surrounded regions.
A ‘O’ is surrounded if there is no path from it to the outer border of the matrix (i.e: row: index 0, column: index 0, row: index matrix.length-1, column: index matrix[0].length-1) when moving in a North, South, East, or West direction.
Basically:
A 'O' will not be flipped to 'X' if:
It is on the border, OR
It is connected to any other 'O' that cannot be flipped
In this solution we get all ‘O’ cells around the borders and keep track of all ‘O’ cells connected to the ones around the outer border.
We mark the border ‘O’ cells, and all the connected ‘O’ cells to the ones around the outer border as invalid.
In the end, we mark all valid ‘O’ cells as ‘X’.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 |
// ============================================================================ // Author: Kenneth Perkins // Date: Nov 1, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to flip surrounded regions // ============================================================================ public class Solution { public void Solve(char[][] board) { var queue = new Queue<KeyValuePair<int, int>>(); // Get coordinates of 'O' cells on the left and right border and add to queue for (int row = 0; row < board.Length; ++row) { // Check left border if (board[row][0] == 'O') { queue.Enqueue(new KeyValuePair<int, int>(row, 0)); } // Check right border if(board[row][board[row].Length - 1] == 'O') { queue.Enqueue(new KeyValuePair<int, int>(row, board[row].Length - 1)); } } // Get coordinates of 'O' cells on the top and bottom border and add to queue for (int col = 0; col < board[0].Length; ++col) { // Check top border if (board[0][col] == 'O') { queue.Enqueue(new KeyValuePair<int, int>(0, col)); } // Check bottom border if (board[board.Length - 1][col] == 'O') { queue.Enqueue(new KeyValuePair<int, int>(board.Length - 1, col)); } } // 2D bool array to keep track of 'O' cells connected to the ones on the outer border var visited = new bool[board.Length][]; for (int row = 0; row < board.Length; ++row) { visited[row] = new bool[board[row].Length]; } // Search directions var directions = new List<KeyValuePair<int, int>>() { // Right new KeyValuePair<int, int>(0, 1), // Left new KeyValuePair<int, int>(0, -1), // Top new KeyValuePair<int, int>(-1, 0), // Bottom new KeyValuePair<int, int>(1, 0), }; // Find all 'O' cells connected to the ones on the outer border while (queue.Count > 0) { var current = queue.Dequeue(); // Get current coordinates var currentRow = current.Key; var currentCol = current.Value; // Mark cell as visited, which means its connected to a border cell visited[currentRow][currentCol] = true; // Search right, left, top, bottom for connected 'O' cells foreach (var direction in directions) { var newRow = currentRow + direction.Key; var newCol = currentCol + direction.Value; // Add connected cells to the queue if (IsValidCell(board, newRow, newCol) && board[newRow][newCol] == 'O' && !visited[newRow][newCol]) { queue.Enqueue(new KeyValuePair<int, int>(newRow, newCol)); } } } // Mark the 'O' cells not connected to outer borders as X for (int row = 0; row < board.Length; ++row) { for (int col = 0; col < board[row].Length; ++col) { if (board[row][col] == 'O' && !visited[row][col]) { board[row][col] = 'X'; } } } } private bool IsValidCell(char[][] board, int row, int col) { return row >= 0 && row < board.Length && col >= 0 && col < board[row].Length; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
[["X"]]












