c-sharp – My Programming Notes

Tag Archives: c-sharp

C# || How To Split Linked List In Parts Using C#

February 01, 2025 admin No comments

The following is a module with functions which demonstrates how to split linked list in parts using C#.

1. Split Linked List In Parts – Problem Statement

Given the head of a singly linked list and an integer k, split the linked list into k consecutive linked list parts.

The length of each part should be as equal as possible: no two parts should have a size differing by more than one. This may lead to some parts being null.

The parts should be in the order of occurrence in the input list, and parts occurring earlier should always have a size greater than or equal to parts occurring later.

Return an array of the k parts.

Example 1:

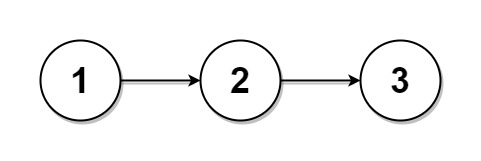
Input: head = [1,2,3], k = 5 Output: [[1],[2],[3],[],[]] Explanation: The first element output[0] has output[0].val = 1, output[0].next = null. The last element output[4] is null, but its string representation as a ListNode is [].

Example 2:

Input: head = [1,2,3,4,5,6,7,8,9,10], k = 3 Output: [[1,2,3,4],[5,6,7],[8,9,10]] Explanation: The input has been split into consecutive parts with size difference at most 1, and earlier parts are a larger size than the later parts.

2. Split Linked List In Parts – Solution

The following is a solution which demonstrates how to split linked list in parts.





		
		
			2. Split Linked List In Parts - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Feb 1, 2025
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to split linked list in parts
// ============================================================================
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     public int val;
 *     public ListNode next;
 *     public ListNode(int val=0, ListNode next=null) {
 *         this.val = val;
 *         this.next = next;
 *     }
 * }
 */
public class Solution {
    public ListNode[] SplitListToParts(ListNode head, int k) {
        // Save nodes to a list
        var items = new List<ListNode>();
        for (var iter = head; iter != null; iter = iter.next) {
            items.Add(iter);
        }

        // Create result array
        var result = new ListNode[k];

        // Determine the size of each batch
        var batchLength = (int)(items.Count / k);

        // Get the remainder
        var remainder = items.Count % k;

        var firstNodeIndex = 0;
        for (int index = 0; index < Math.Min(k, items.Count); ++index) {
            var currentBatchLength = batchLength;
            if (index < remainder) {
                currentBatchLength += 1;
            }

            var lastNodeIndex = firstNodeIndex + (currentBatchLength - 1);

            // Get the head and tail nodes for this batch
            var batchHead = items[firstNodeIndex];
            var batchTail = items[lastNodeIndex];

            // Set the tail to null
            batchTail.next = null;

            // Save the head to the result array
            result[index] = batchHead;

            // Increment the first node index
            firstNodeIndex = lastNodeIndex + 1;
        }

        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Feb 1, 2025
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to split linked list in parts
// ============================================================================
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     public int val;
 *     public ListNode next;
 *     public ListNode(int val=0, ListNode next=null) {
 *         this.val = val;
 *         this.next = next;
 *     }
 * }
 */
public class Solution {
    public ListNode[] SplitListToParts(ListNode head, int k) {
        // Save nodes to a list
        var items = new List<ListNode>();
        for (var iter = head; iter != null; iter = iter.next) {
            items.Add(iter);
        }
 
        // Create result array
        var result = new ListNode[k];
 
        // Determine the size of each batch
        var batchLength = (int)(items.Count / k);
 
        // Get the remainder
        var remainder = items.Count % k;
 
        var firstNodeIndex = 0;
        for (int index = 0; index < Math.Min(k, items.Count); ++index) {
            var currentBatchLength = batchLength;
            if (index < remainder) {
                currentBatchLength += 1;
            }
 
            var lastNodeIndex = firstNodeIndex + (currentBatchLength - 1);
 
            // Get the head and tail nodes for this batch
            var batchHead = items[firstNodeIndex];
            var batchTail = items[lastNodeIndex];
 
            // Set the tail to null
            batchTail.next = null;
 
            // Save the head to the result array
            result[index] = batchHead;
 
            // Increment the first node index
            firstNodeIndex = lastNodeIndex + 1;
        }
 
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[[1],[2],[3],[],[]] [[1,2,3,4],[5,6,7],[8,9,10]]

C# || How To Get First X Rows of Pascal’s Triangle Using C#

January 01, 2025 admin No comments

The following is a module with functions which demonstrates how to get first x rows of Pascal’s Triangle using C#.

1. Pascal’s Triangle – Problem Statement

Given an integer numRows, return the first numRows of Pascal’s triangle.

In Pascal’s triangle, each number is the sum of the two numbers directly above it as shown:

Example 1:

Input: numRows = 5 Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

Example 2:

Input: numRows = 1 Output: [[1]]

2. Pascal’s Triangle – Solution

The following is a solution which demonstrates how to convert get first x rows of Pascal’s Triangle.





		
		
			2. Pascal's Triangle - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jan 1, 2025
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get first x rows of Pascal's Triangle
// ============================================================================
public class Solution {
    public IList<IList<int>> Generate(int numRows) {
        var results = new List<IList<int>>();
        if (numRows < 1) {
            return results;
        }

        // Add the initial row
        results.Add(new List<int>() {
            {1}
        });

        for (int row = 2; row <= numRows; ++row) {
            var previousRow = results[results.Count - 1];
            var currentRow = new List<int>();
            currentRow.Add(previousRow[0]);
            for (int index = 1; index < row - 1; ++index) {
                var value = previousRow[index - 1] + previousRow[index];
                currentRow.Add(value);
            }
            currentRow.Add(previousRow[previousRow.Count - 1]);
            results.Add(currentRow);
        }
        return results;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jan 1, 2025
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get first x rows of Pascal's Triangle
// ============================================================================
public class Solution {
    public IList<IList<int>> Generate(int numRows) {
        var results = new List<IList<int>>();
        if (numRows < 1) {
            return results;
        }
 
        // Add the initial row
        results.Add(new List<int>() {
            {1}
        });
 
        for (int row = 2; row <= numRows; ++row) {
            var previousRow = results[results.Count - 1];
            var currentRow = new List<int>();
            currentRow.Add(previousRow[0]);
            for (int index = 1; index < row - 1; ++index) {
                var value = previousRow[index - 1] + previousRow[index];
                currentRow.Add(value);
            }
            currentRow.Add(previousRow[previousRow.Count - 1]);
            results.Add(currentRow);
        }
        return results;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]] [[1]]

C# || How To Get Smallest String Starting From Leaf Using C#

December 01, 2024 admin No comments

The following is a module with functions which demonstrates how to get smallest string starting from leaf using C#.

1. Smallest String Starting From Leaf – Problem Statement

You are given the root of a binary tree where each node has a value in the range [0, 25] representing the letters 'a' to 'z'.

Return the lexicographically smallest string that starts at a leaf of this tree and ends at the root.

As a reminder, any shorter prefix of a string is lexicographically smaller.

For example, "ab" is lexicographically smaller than "aba".

A leaf of a node is a node that has no children.

Example 1:

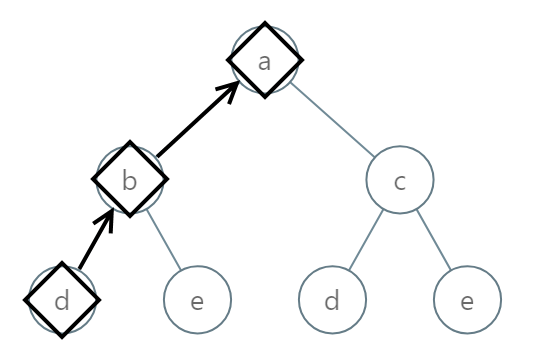
Input: root = [0,1,2,3,4,3,4] Output: "dba"

Example 2:

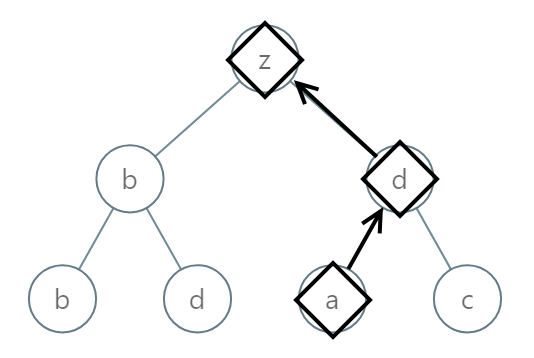
Input: root = [25,1,3,1,3,0,2] Output: "adz"

Example 3:

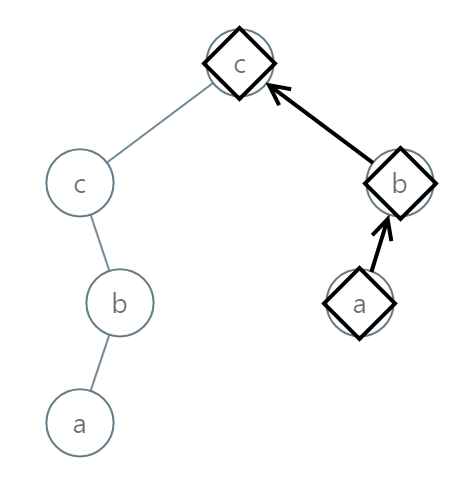
Input: root = [2,2,1,null,1,0,null,0] Output: "abc"

2. Smallest String Starting From Leaf – Solution

The following is a solution which demonstrates how to convert get smallest string starting from leaf.





		
		
			2. Smallest String Starting From Leaf - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Dec 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get smallest string starting from leaf
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public string SmallestFromLeaf(TreeNode root) {
        var smallestString = "";
        var queue = new Queue<KeyValuePair<TreeNode, string>>();

        // Enqueue root node to queue along with its value converted to a character
        queue.Enqueue(new KeyValuePair<TreeNode, string>(root, ((char)(root.val + 'a')).ToString()));

        // Perform BFS traversal until queue is empty
        while (queue.Count > 0) {

            // Pop the leftmost node and its corresponding string from queue
            var pair = queue.Dequeue();
            var node = pair.Key;
            var currentString = pair.Value;

            // If current node is a leaf node
            if (node.left == null && node.right == null) {

                // Update smallest_string if it's empty or current string is smaller
                if (string.IsNullOrEmpty(smallestString)) {
                    smallestString = currentString;
                } else {
                    smallestString = currentString.CompareTo(smallestString) < 0 ? currentString : smallestString;
                }
            }

            // If current node has a left child, append it to queue
            if (node.left != null) {
                queue.Enqueue(new KeyValuePair<TreeNode, string>(node.left, (char)(node.left.val + 'a') + currentString));
            }

            // If current node has a right child, append it to queue
            if (node.right != null) {
                queue.Enqueue(new KeyValuePair<TreeNode, string>(node.right, (char)(node.right.val + 'a') + currentString));
            }
        }

        return smallestString;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Dec 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get smallest string starting from leaf
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public string SmallestFromLeaf(TreeNode root) {
        var smallestString = "";
        var queue = new Queue<KeyValuePair<TreeNode, string>>();
 
        // Enqueue root node to queue along with its value converted to a character
        queue.Enqueue(new KeyValuePair<TreeNode, string>(root, ((char)(root.val + 'a')).ToString()));
 
        // Perform BFS traversal until queue is empty
        while (queue.Count > 0) {
 
            // Pop the leftmost node and its corresponding string from queue
            var pair = queue.Dequeue();
            var node = pair.Key;
            var currentString = pair.Value;
 
            // If current node is a leaf node
            if (node.left == null && node.right == null) {
 
                // Update smallest_string if it's empty or current string is smaller
                if (string.IsNullOrEmpty(smallestString)) {
                    smallestString = currentString;
                } else {
                    smallestString = currentString.CompareTo(smallestString) < 0 ? currentString : smallestString;
                }
            }
 
            // If current node has a left child, append it to queue
            if (node.left != null) {
                queue.Enqueue(new KeyValuePair<TreeNode, string>(node.left, (char)(node.left.val + 'a') + currentString));
            }
 
            // If current node has a right child, append it to queue
            if (node.right != null) {
                queue.Enqueue(new KeyValuePair<TreeNode, string>(node.right, (char)(node.right.val + 'a') + currentString));
            }
        }
 
        return smallestString;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

"dba" "adz" "abc"

C# || How To Convert Integer To English Words Using C#

November 01, 2024 admin No comments

The following is a module with functions which demonstrates how to convert integer to english words using C#.

1. Integer to English Words – Problem Statement

Convert a non-negative integer num to its English words representation.

Example 1:

Input: num = 123 Output: "One Hundred Twenty Three"

Example 2:

Input: num = 12345 Output: "Twelve Thousand Three Hundred Forty Five"

Example 3:

Input: num = 1234567 Output: "One Million Two Hundred Thirty Four Thousand Five Hundred Sixty Seven"

2. Integer to English Words – Solution

The following is a solution which demonstrates how to convert integer to english words.





		
		
			2. Integer to English Words - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to convert integer to english word
// ============================================================================
public class NumberWord {
    public int Value { get; }
    public string Word { get; }

    public NumberWord(int value, string word) {
        Value = value;
        Word = word;
    }
}

public class Solution {
    // List to store words for numbers
    private static readonly List<NumberWord> numberToWordsList = new List<NumberWord> {
        new NumberWord(1000000000, "Billion"),
        new NumberWord(1000000, "Million"),
        new NumberWord(1000, "Thousand"),
        new NumberWord(100, "Hundred"),
        new NumberWord(90, "Ninety"),
        new NumberWord(80, "Eighty"),
        new NumberWord(70, "Seventy"),
        new NumberWord(60, "Sixty"),
        new NumberWord(50, "Fifty"),
        new NumberWord(40, "Forty"),
        new NumberWord(30, "Thirty"),
        new NumberWord(20, "Twenty"),
        new NumberWord(19, "Nineteen"),
        new NumberWord(18, "Eighteen"),
        new NumberWord(17, "Seventeen"),
        new NumberWord(16, "Sixteen"),
        new NumberWord(15, "Fifteen"),
        new NumberWord(14, "Fourteen"),
        new NumberWord(13, "Thirteen"),
        new NumberWord(12, "Twelve"),
        new NumberWord(11, "Eleven"),
        new NumberWord(10, "Ten"),
        new NumberWord(9, "Nine"),
        new NumberWord(8, "Eight"),
        new NumberWord(7, "Seven"),
        new NumberWord(6, "Six"),
        new NumberWord(5, "Five"),
        new NumberWord(4, "Four"),
        new NumberWord(3, "Three"),
        new NumberWord(2, "Two"),
        new NumberWord(1, "One")
    };

    public string NumberToWords(int num) {
        if (num == 0) {
            return "Zero";
        }

        foreach (var nw in numberToWordsList) {
            // Check if the number is greater than or equal to the current unit
            if (num >= nw.Value) {
                // Convert the quotient to words if the current unit is 100 or greater
                string prefix = (num >= 100) ? NumberToWords(num / nw.Value) + " " : "";

                // Get the word for the current unit
                string unit = nw.Word;

                // Convert the remainder to words if it's not zero
                string suffix = (num % nw.Value == 0) ? "" : " " + NumberToWords(num % nw.Value);

                return prefix + unit + suffix;
            }
        }

        return "";
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to convert integer to english word
// ============================================================================
public class NumberWord {
    public int Value { get; }
    public string Word { get; }
 
    public NumberWord(int value, string word) {
        Value = value;
        Word = word;
    }
}
 
public class Solution {
    // List to store words for numbers
    private static readonly List<NumberWord> numberToWordsList = new List<NumberWord> {
        new NumberWord(1000000000, "Billion"),
        new NumberWord(1000000, "Million"),
        new NumberWord(1000, "Thousand"),
        new NumberWord(100, "Hundred"),
        new NumberWord(90, "Ninety"),
        new NumberWord(80, "Eighty"),
        new NumberWord(70, "Seventy"),
        new NumberWord(60, "Sixty"),
        new NumberWord(50, "Fifty"),
        new NumberWord(40, "Forty"),
        new NumberWord(30, "Thirty"),
        new NumberWord(20, "Twenty"),
        new NumberWord(19, "Nineteen"),
        new NumberWord(18, "Eighteen"),
        new NumberWord(17, "Seventeen"),
        new NumberWord(16, "Sixteen"),
        new NumberWord(15, "Fifteen"),
        new NumberWord(14, "Fourteen"),
        new NumberWord(13, "Thirteen"),
        new NumberWord(12, "Twelve"),
        new NumberWord(11, "Eleven"),
        new NumberWord(10, "Ten"),
        new NumberWord(9, "Nine"),
        new NumberWord(8, "Eight"),
        new NumberWord(7, "Seven"),
        new NumberWord(6, "Six"),
        new NumberWord(5, "Five"),
        new NumberWord(4, "Four"),
        new NumberWord(3, "Three"),
        new NumberWord(2, "Two"),
        new NumberWord(1, "One")
    };
 
    public string NumberToWords(int num) {
        if (num == 0) {
            return "Zero";
        }
 
        foreach (var nw in numberToWordsList) {
            // Check if the number is greater than or equal to the current unit
            if (num >= nw.Value) {
                // Convert the quotient to words if the current unit is 100 or greater
                string prefix = (num >= 100) ? NumberToWords(num / nw.Value) + " " : "";
 
                // Get the word for the current unit
                string unit = nw.Word;
 
                // Convert the remainder to words if it's not zero
                string suffix = (num % nw.Value == 0) ? "" : " " + NumberToWords(num % nw.Value);
 
                return prefix + unit + suffix;
            }
        }
 
        return "";
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

"One Hundred Twenty Three" "Twelve Thousand Three Hundred Forty Five" "One Million Two Hundred Thirty Four Thousand Five Hundred Sixty Seven"

C# || How To Find Mode In Binary Search Tree Using C#

October 01, 2024 admin No comments

The following is a module with functions which demonstrates how to find mode in binary search tree using C#.

1. Find Mode – Problem Statement

Given the root of a binary search tree (BST) with duplicates, return all the mode(s) (i.e., the most frequently occurred element) in it.

If the tree has more than one mode, return them in any order.

Assume a BST is defined as follows:

The left subtree of a node contains only nodes with keys less than or equal to the node’s key.
The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
Both the left and right subtrees must also be binary search trees.

Example 1:

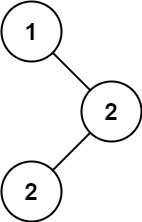
Input: root = [1,null,2,2] Output: [2]

Example 2:

Input: root = [0] Output: [0]

2. Find Mode – Solution

The following is a solution which demonstrates how to find mode in binary search tree.





		
		
			2. Find Mode - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find mode in binary search tree
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int[] FindMode(TreeNode root) {
        int maxStreak = 0;
        int currStreak = 0;
        int currNum = 0;
        var ans = new List<int>();

        TreeNode curr = root;
        while (curr != null) {
            if (curr.left != null) {
                // Find the friend
                TreeNode friend = curr.left;
                while (friend.right != null) {
                    friend = friend.right;
                }

                friend.right = curr;

                // Delete the edge after using it
                TreeNode left = curr.left;
                curr.left = null;
                curr = left;
            } else {
                // Handle the current node
                int num = curr.val;
                if (num == currNum) {
                    currStreak++;
                } else {
                    currStreak = 1;
                    currNum = num;
                }

                if (currStreak > maxStreak) {
                    ans = new List<int>();
                    maxStreak = currStreak;
                }

                if (currStreak == maxStreak) {
                    ans.Add(num);
                }

                curr = curr.right;
            }
        }


        int[] result = new int[ans.Count];
        for (int i = 0; i < ans.Count; i++) {
            result[i] = ans[i];
        }

        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find mode in binary search tree
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int[] FindMode(TreeNode root) {
        int maxStreak = 0;
        int currStreak = 0;
        int currNum = 0;
        var ans = new List<int>();
 
        TreeNode curr = root;
        while (curr != null) {
            if (curr.left != null) {
                // Find the friend
                TreeNode friend = curr.left;
                while (friend.right != null) {
                    friend = friend.right;
                }
 
                friend.right = curr;
 
                // Delete the edge after using it
                TreeNode left = curr.left;
                curr.left = null;
                curr = left;
            } else {
                // Handle the current node
                int num = curr.val;
                if (num == currNum) {
                    currStreak++;
                } else {
                    currStreak = 1;
                    currNum = num;
                }
 
                if (currStreak > maxStreak) {
                    ans = new List<int>();
                    maxStreak = currStreak;
                }
 
                if (currStreak == maxStreak) {
                    ans.Add(num);
                }
 
                curr = curr.right;
            }
        }
 
 
        int[] result = new int[ans.Count];
        for (int i = 0; i < ans.Count; i++) {
            result[i] = ans[i];
        }
 
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[2] [0]

C# || How To Find The Winner Of Array Game Using C#

September 01, 2024 admin No comments

The following is a module with functions which demonstrates how to find the winner of array game using C#.

1. Get Winner – Problem Statement

Given an integer array arr of distinct integers and an integer k.

A game will be played between the first two elements of the array (i.e. arr[0] and arr[1]). In each round of the game, we compare arr[0] with arr[1], the larger integer wins and remains at position 0, and the smaller integer moves to the end of the array. The game ends when an integer wins k consecutive rounds.

Return the integer which will win the game.

It is guaranteed that there will be a winner of the game.

Example 1:

Input: arr = [2,1,3,5,4,6,7], k = 2 Output: 5 Explanation: Let's see the rounds of the game: Round | arr | winner | win_count 1 | [2,1,3,5,4,6,7] | 2 | 1 2 | [2,3,5,4,6,7,1] | 3 | 1 3 | [3,5,4,6,7,1,2] | 5 | 1 4 | [5,4,6,7,1,2,3] | 5 | 2 So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.

Example 2:

Input: arr = [3,2,1], k = 10 Output: 3 Explanation: 3 will win the first 10 rounds consecutively.

2. Get Winner – Solution

The following is a solution which demonstrates how to find the winner of array game.





		
		
			2. Get Winner - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Sep 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the winner of array game
// ============================================================================
public class Solution {
    public int GetWinner(int[] arr, int k) {
        int maxElement = arr[0];
        for (int index = 1; index < arr.Length; ++index) {
            maxElement = Math.Max(maxElement, arr[index]);
        }

        int curr = arr[0];
        int winstreak = 0;

        for (int index = 1; index < arr.Length; ++index) {
            int opponent = arr[index];

            if (curr > opponent) {
                ++winstreak;
            } else {
                curr = opponent;
                winstreak = 1;
            }

            if (winstreak == k || curr == maxElement) {
                return curr;
            }
        }

        return -1;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Sep 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the winner of array game
// ============================================================================
public class Solution {
    public int GetWinner(int[] arr, int k) {
        int maxElement = arr[0];
        for (int index = 1; index < arr.Length; ++index) {
            maxElement = Math.Max(maxElement, arr[index]);
        }
 
        int curr = arr[0];
        int winstreak = 0;
 
        for (int index = 1; index < arr.Length; ++index) {
            int opponent = arr[index];
 
            if (curr > opponent) {
                ++winstreak;
            } else {
                curr = opponent;
                winstreak = 1;
            }
 
            if (winstreak == k || curr == maxElement) {
                return curr;
            }
        }
 
        return -1;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

5 3

C# || How To Design Seat Reservation Manager Using C#

August 01, 2024 admin No comments

The following is a module with functions which demonstrates how to design a seat reservation manager using C#.

1. Seat Manager – Problem Statement

Design a system that manages the reservation state of n seats that are numbered from 1 to n.

Implement the SeatManager class:

SeatManager(int n) Initializes a SeatManager object that will manage n seats numbered from 1 to n. All seats are initially available.
int reserve() Fetches the smallest-numbered unreserved seat, reserves it, and returns its number.
void unreserve(int seatNumber) Unreserves the seat with the given seatNumber.

Example 1:

Input ["SeatManager", "reserve", "reserve", "unreserve", "reserve", "reserve", "reserve", "reserve", "unreserve"] [[5], [], [], [2], [], [], [], [], [5]] Output [null, 1, 2, null, 2, 3, 4, 5, null]
Explanation SeatManager seatManager = new SeatManager(5); // Initializes a SeatManager with 5 seats. seatManager.reserve(); // All seats are available, so return the lowest numbered seat, which is 1. seatManager.reserve(); // The available seats are [2,3,4,5], so return the lowest of them, which is 2. seatManager.unreserve(2); // Unreserve seat 2, so now the available seats are [2,3,4,5]. seatManager.reserve(); // The available seats are [2,3,4,5], so return the lowest of them, which is 2. seatManager.reserve(); // The available seats are [3,4,5], so return the lowest of them, which is 3. seatManager.reserve(); // The available seats are [4,5], so return the lowest of them, which is 4. seatManager.reserve(); // The only available seat is seat 5, so return 5. seatManager.unreserve(5); // Unreserve seat 5, so now the available seats are [5].

2. Seat Manager – Solution

The following is a solution which demonstrates how to design a seat reservation manager.





		
		
			2. Seat Manager - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Aug 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to design a seat reservation manager
// ============================================================================
/**
 * Your SeatManager object will be instantiated and called as such:
 * SeatManager obj = new SeatManager(n);
 * int param_1 = obj.Reserve();
 * obj.Unreserve(seatNumber);
 */
public class SeatManager {
    // Marker to point to unreserved seats.
    int marker;

    // Sorted set to store all unreserved seats.
    SortedSet<int> availableSeats;

    public SeatManager(int n) {
        // Set marker to the first unreserved seat.
        marker = 1;
        // Initialize the sorted set.
        availableSeats = new SortedSet<int>();
    }

    public int Reserve() {
        // If the sorted set has any element in it, then,
        // get the smallest-numbered unreserved seat from it.
        if (availableSeats.Count > 0) {
            int firstSeatNumber = availableSeats.First();
            availableSeats.Remove(firstSeatNumber);
            return firstSeatNumber;
        }

        // Otherwise, the marker points to the smallest-numbered seat.
        int seatNumber = marker;
        marker++;
        return seatNumber;
    }

    public void Unreserve(int seatNumber) {
        // Push the unreserved seat in the sorted set.
        availableSeats.Add(seatNumber);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Aug 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to design a seat reservation manager
// ============================================================================
/**
 * Your SeatManager object will be instantiated and called as such:
 * SeatManager obj = new SeatManager(n);
 * int param_1 = obj.Reserve();
 * obj.Unreserve(seatNumber);
 */
public class SeatManager {
    // Marker to point to unreserved seats.
    int marker;
 
    // Sorted set to store all unreserved seats.
    SortedSet<int> availableSeats;
 
    public SeatManager(int n) {
        // Set marker to the first unreserved seat.
        marker = 1;
        // Initialize the sorted set.
        availableSeats = new SortedSet<int>();
    }
 
    public int Reserve() {
        // If the sorted set has any element in it, then,
        // get the smallest-numbered unreserved seat from it.
        if (availableSeats.Count > 0) {
            int firstSeatNumber = availableSeats.First();
            availableSeats.Remove(firstSeatNumber);
            return firstSeatNumber;
        }
 
        // Otherwise, the marker points to the smallest-numbered seat.
        int seatNumber = marker;
        marker++;
        return seatNumber;
    }
 
    public void Unreserve(int seatNumber) {
        // Push the unreserved seat in the sorted set.
        availableSeats.Add(seatNumber);
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[null,1,2,null,2,3,4,5,null]

C# || How To Restore Array From Adjacent Pairs Using C#

July 28, 2024 admin No comments

The following is a module with functions which demonstrates how to restore the array from adjacent pairs using C#.

1. Restore Array – Problem Statement

There is an integer array nums that consists of n unique elements, but you have forgotten it. However, you do remember every pair of adjacent elements in nums.

You are given a 2D integer array adjacentPairs of size n – 1 where each adjacentPairs[i] = [u_i, v_i] indicates that the elements u_i and v_i are adjacent in nums.

It is guaranteed that every adjacent pair of elements nums[i] and nums[i+1] will exist in adjacentPairs, either as [nums[i], nums[i+1]] or [nums[i+1], nums[i]]. The pairs can appear in any order.

Return the original array nums. If there are multiple solutions, return any of them.

Example 1:

Input: adjacentPairs = [[2,1],[3,4],[3,2]] Output: [1,2,3,4] Explanation: This array has all its adjacent pairs in adjacentPairs. Notice that adjacentPairs[i] may not be in left-to-right order.

Example 2:

Input: adjacentPairs = [[4,-2],[1,4],[-3,1]] Output: [-2,4,1,-3] Explanation: There can be negative numbers. Another solution is [-3,1,4,-2], which would also be accepted.

Example 3:

Input: adjacentPairs = [[100000,-100000]] Output: [100000,-100000]

2. Restore Array – Solution

The following is a solution which demonstrates how to restore the array from adjacent pairs.





		
		
			2. Restore Array - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jul 28, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to restore the array from adjacent pairs
// ============================================================================
public class Solution {
    public int[] RestoreArray(int[][] adjacentPairs) {
        var graph = new Dictionary<int, List<int>>();

        foreach (int[] edge in adjacentPairs) {
            int x = edge[0];
            int y = edge[1];

            if (!graph.ContainsKey(x)) {
                graph[x] = new List<int>();
            }

            if (!graph.ContainsKey(y)) {
                graph[y] = new List<int>();
            }

            graph[x].Add(y);
            graph[y].Add(x);
        }

        int root = 0;
        foreach (int num in graph.Keys) {
            if (graph[num].Count == 1) {
                root = num;
                break;
            }
        }

        int curr = root;
        int[] ans = new int[graph.Count];
        ans[0] = root;
        int i = 1;
        int prev = int.MaxValue;

        while (i < graph.Count) {
            foreach (int neighbor in graph[curr]) {
                if (neighbor != prev) {
                    ans[i] = neighbor;
                    i++;
                    prev = curr;
                    curr = neighbor;
                    break;
                }
            }
        }

        return ans;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jul 28, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to restore the array from adjacent pairs
// ============================================================================
public class Solution {
    public int[] RestoreArray(int[][] adjacentPairs) {
        var graph = new Dictionary<int, List<int>>();
 
        foreach (int[] edge in adjacentPairs) {
            int x = edge[0];
            int y = edge[1];
 
            if (!graph.ContainsKey(x)) {
                graph[x] = new List<int>();
            }
 
            if (!graph.ContainsKey(y)) {
                graph[y] = new List<int>();
            }
 
            graph[x].Add(y);
            graph[y].Add(x);
        }
 
        int root = 0;
        foreach (int num in graph.Keys) {
            if (graph[num].Count == 1) {
                root = num;
                break;
            }
        }
 
        int curr = root;
        int[] ans = new int[graph.Count];
        ans[0] = root;
        int i = 1;
        int prev = int.MaxValue;
 
        while (i < graph.Count) {
            foreach (int neighbor in graph[curr]) {
                if (neighbor != prev) {
                    ans[i] = neighbor;
                    i++;
                    prev = curr;
                    curr = neighbor;
                    break;
                }
            }
        }
 
        return ans;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[1,2,3,4] [-2,4,1,-3] [100000,-100000]

C# || How To Design Graph With Shortest Path Calculator Using C#

June 01, 2024 admin No comments

The following is a module with functions which demonstrates how to design graph with shortest path calculator using C#.

1. Graph – Problem Statement

There is a directed weighted graph that consists of n nodes numbered from 0 to n – 1. The edges of the graph are initially represented by the given array edges where edges[i] = [from_i, to_i, edgeCost_i] meaning that there is an edge from from_i to to_i with the cost edgeCost_i.

Implement the Graph class:

Graph(int n, int[][] edges) initializes the object with n nodes and the given edges.
addEdge(int[] edge) adds an edge to the list of edges where edge = [from, to, edgeCost]. It is guaranteed that there is no edge between the two nodes before adding this one.
int shortestPath(int node1, int node2) returns the minimum cost of a path from node1 to node2. If no path exists, return -1. The cost of a path is the sum of the costs of the edges in the path.

Example 1:

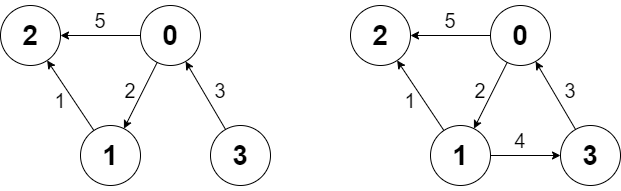
Input ["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"] [[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]] Output [null, 6, -1, null, 6]
Explanation Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]); g.shortestPath(3, 2); // return 6. The shortest path from 3 to 2 in the first diagram above is 3 -> 0 -> 1 -> 2 with a total cost of 3 + 2 + 1 = 6. g.shortestPath(0, 3); // return -1. There is no path from 0 to 3. g.addEdge([1, 3, 4]); // We add an edge from node 1 to node 3, and we get the second diagram above. g.shortestPath(0, 3); // return 6. The shortest path from 0 to 3 now is 0 -> 1 -> 3 with a total cost of 2 + 4 = 6.

2. Graph – Solution

The following is a solution which demonstrates how to design graph with shortest path calculator.





		
		
			2. Graph - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jun 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to design graph shortest path calculator
// ============================================================================
/**
 * Your Graph object will be instantiated and called as such:
 * Graph obj = new Graph(n, edges);
 * obj.AddEdge(edge);
 * int param_2 = obj.ShortestPath(node1,node2);
 */
public class Graph {
    List<List<KeyValuePair<int, int>>> adjList;

    public Graph(int n, int[][] edges) {
        adjList = new List<List<KeyValuePair<int, int>>>();
        for (int i = 0; i < n; i++) {
            adjList.Add(new List<KeyValuePair<int, int>>());
        }
        foreach (int[] e in edges) {
            AddEdge(e);
        }
    }

    public void AddEdge(int[] edge) {
        adjList[edge[0]].Add(new KeyValuePair<int, int>(edge[1], edge[2]));
    }

    public int ShortestPath(int node1, int node2) {
        int n = adjList.Count;
        var pq = new PriorityQueue<List<int>, List<int>>(
            Comparer<List<int>>.Create((a, b) => a[0].CompareTo(b[0]))
        );

        int[] costForNode = new int[n];
        Array.Fill(costForNode, int.MaxValue);
        costForNode[node1] = 0;

        var root = new List<int>() { 0, node1 };
        pq.Enqueue(root, root);

        while (pq.Count > 0) {
            var curr = pq.Dequeue();
            int currCost = curr[0];
            int currNode = curr[1];

            if (currCost > costForNode[currNode]) {
                continue;
            }
            if (currNode == node2) {
                return currCost;
            }
            foreach (var neighbor in adjList[currNode]) {
                int neighborNode = neighbor.Key;
                int cost = neighbor.Value;
                int newCost = currCost + cost;

                if (newCost < costForNode[neighborNode]) {
                    costForNode[neighborNode] = newCost;
                    var newPath = new List<int>() { newCost, neighborNode };
                    pq.Enqueue(newPath, newPath);
                }
            }
        }

        return -1;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jun 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to design graph shortest path calculator
// ============================================================================
/**
 * Your Graph object will be instantiated and called as such:
 * Graph obj = new Graph(n, edges);
 * obj.AddEdge(edge);
 * int param_2 = obj.ShortestPath(node1,node2);
 */
public class Graph {
    List<List<KeyValuePair<int, int>>> adjList;
 
    public Graph(int n, int[][] edges) {
        adjList = new List<List<KeyValuePair<int, int>>>();
        for (int i = 0; i < n; i++) {
            adjList.Add(new List<KeyValuePair<int, int>>());
        }
        foreach (int[] e in edges) {
            AddEdge(e);
        }
    }
 
    public void AddEdge(int[] edge) {
        adjList[edge[0]].Add(new KeyValuePair<int, int>(edge[1], edge[2]));
    }
 
    public int ShortestPath(int node1, int node2) {
        int n = adjList.Count;
        var pq = new PriorityQueue<List<int>, List<int>>(
            Comparer<List<int>>.Create((a, b) => a[0].CompareTo(b[0]))
        );
 
        int[] costForNode = new int[n];
        Array.Fill(costForNode, int.MaxValue);
        costForNode[node1] = 0;
 
        var root = new List<int>() { 0, node1 };
        pq.Enqueue(root, root);
 
        while (pq.Count > 0) {
            var curr = pq.Dequeue();
            int currCost = curr[0];
            int currNode = curr[1];
 
            if (currCost > costForNode[currNode]) {
                continue;
            }
            if (currNode == node2) {
                return currCost;
            }
            foreach (var neighbor in adjList[currNode]) {
                int neighborNode = neighbor.Key;
                int cost = neighbor.Value;
                int newCost = currCost + cost;
 
                if (newCost < costForNode[neighborNode]) {
                    costForNode[neighborNode] = newCost;
                    var newPath = new List<int>() { newCost, neighborNode };
                    pq.Enqueue(newPath, newPath);
                }
            }
        }
 
        return -1;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[null,6,-1,null,6]

C# || How To Find Largest 3 Same Digit Number In String Using C#

May 23, 2024 admin No comments

The following is a module with functions which demonstrates how to find the largest 3 same digit number in a string using C#.

1. Largest Good Integer – Problem Statement

You are given a string num representing a large integer. An integer is good if it meets the following conditions:

It is a substring of num with length 3.
It consists of only one unique digit.

Return the maximum good integer as a string or an empty string “” if no such integer exists.

Note:

A substring is a contiguous sequence of characters within a string.
There may be leading zeroes in num or a good integer.

Example 1:

Input: num = "6777133339" Output: "777" Explanation: There are two distinct good integers: "777" and "333". "777" is the largest, so we return "777".

Example 2:

Input: num = "2300019" Output: "000" Explanation: "000" is the only good integer.

Example 3:

Input: num = "42352338" Output: "" Explanation: No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.

2. Largest Good Integer – Solution

The following is a solution which demonstrates how to find the largest 3 same digit number in a string.





		
		
			2. Largest Good Integer - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   May 23, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find largest odd number in a string
// ============================================================================
public class Solution {
    public string LargestGoodInteger(string num) {
        // Assign 'maxDigit' to the NUL character (smallest ASCII value character)
        char maxDigit = '\0';

        // Iterate on characters of the num string.
        for (int index = 0; index <= num.Length - 3; ++index) {
            // If 3 consecutive characters are the same,
            // store the character in 'maxDigit' if it's bigger than what it already stores.
            if (num[index] == num[index + 1] && num[index] == num[index + 2]) {
                maxDigit = (char) Math.Max(maxDigit, num[index]);
            }
        }

        // If 'maxDigit' is NUL, return an empty string; otherwise, return a string of size 3 with 'maxDigit' characters.
        return maxDigit == '\0' ? "" : new string(new char[]{maxDigit, maxDigit, maxDigit});
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   May 23, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find largest odd number in a string
// ============================================================================
public class Solution {
    public string LargestGoodInteger(string num) {
        // Assign 'maxDigit' to the NUL character (smallest ASCII value character)
        char maxDigit = '\0';
 
        // Iterate on characters of the num string.
        for (int index = 0; index <= num.Length - 3; ++index) {
            // If 3 consecutive characters are the same,
            // store the character in 'maxDigit' if it's bigger than what it already stores.
            if (num[index] == num[index + 1] && num[index] == num[index + 2]) {
                maxDigit = (char) Math.Max(maxDigit, num[index]);
            }
        }
 
        // If 'maxDigit' is NUL, return an empty string; otherwise, return a string of size 3 with 'maxDigit' characters.
        return maxDigit == '\0' ? "" : new string(new char[]{maxDigit, maxDigit, maxDigit});
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

"777" "000" ""

C# || How To Find Largest Odd Number In String Using C#

April 13, 2024 admin No comments

The following is a module with functions which demonstrates how to find the largest odd number in a string using C#.

1. Largest Odd Number – Problem Statement

You are given a string num, representing a large integer. Return the largest-valued odd integer (as a string) that is a non-empty substring of num, or an empty string “” if no odd integer exists.

A substring is a contiguous sequence of characters within a string.

Example 1:

Input: num = "52" Output: "5" Explanation: The only non-empty substrings are "5", "2", and "52". "5" is the only odd number.

Example 2:

Input: num = "4206" Output: "" Explanation: There are no odd numbers in "4206".

Example 3:

Input: num = "35427" Output: "35427" Explanation: "35427" is already an odd number.

2. Largest Odd Number – Solution

The following is a solution which demonstrates how to find the largest odd number in a string.





		
		
			2. Largest Odd Number - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Apr 13, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find largest odd number in a string
// ============================================================================
public class Solution {
    public string LargestOddNumber(string num) {
        for (int index = num.Length - 1; index >= 0; --index) {
            if (Convert.ToInt32(num[index]) % 2 != 0) {
                return num.Substring(0, index + 1);
            }
        }
        return "";
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Apr 13, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find largest odd number in a string
// ============================================================================
public class Solution {
    public string LargestOddNumber(string num) {
        for (int index = num.Length - 1; index >= 0; --index) {
            if (Convert.ToInt32(num[index]) % 2 != 0) {
                return num.Substring(0, index + 1);
            }
        }
        return "";
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

"5" "" "35427"

C# || How To Determine If A Binary Tree Is Even Odd Tree Using C#

March 01, 2024 admin No comments

The following is a module with functions which demonstrates how to determine if a binary tree is an even odd tree using C#.

1. Is Even Odd Tree – Problem Statement

A binary tree is named Even-Odd if it meets the following conditions:

The root of the binary tree is at level index 0, its children are at level index 1, their children are at level index 2, etc.
For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).

Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.

Example 1:

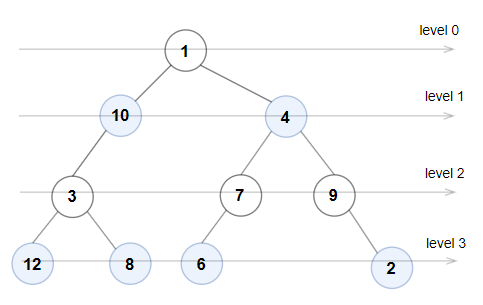
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2] Output: true Explanation: The node values on each level are: Level 0: [1] Level 1: [10,4] Level 2: [3,7,9] Level 3: [12,8,6,2] Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.

Example 2:

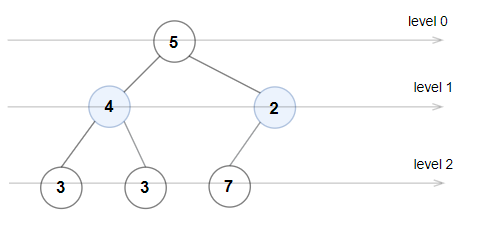
Input: root = [5,4,2,3,3,7] Output: false Explanation: The node values on each level are: Level 0: [5] Level 1: [4,2] Level 2: [3,3,7] Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.

Example 3:

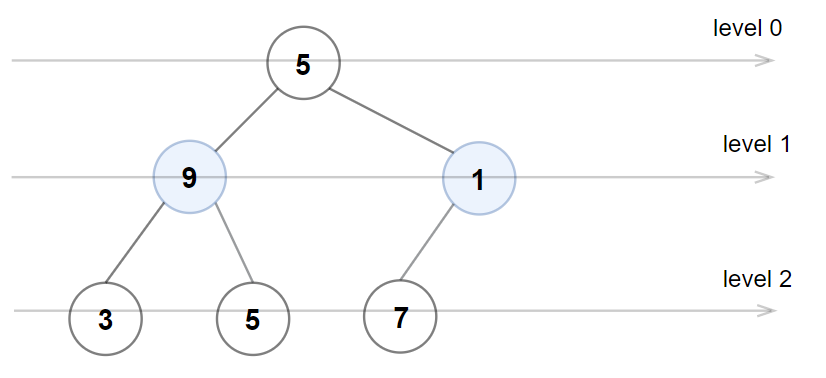
Input: root = [5,9,1,3,5,7] Output: false Explanation: Node values in the level 1 should be even integers.

2. Is Even Odd Tree – Solution

The following is a solution which demonstrates how to determine if a binary tree is an even odd tree.

This solution uses breadth-first search.





		
		
			2. Is Even Odd Tree - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Mar 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to determine an even odd tree
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public bool IsEvenOddTree(TreeNode root) {
        var queue = new Queue<TreeNode>();
        queue.Enqueue(root);

        var isEvenLevel = true;
        while (queue.Count > 0) {
            int previousValue = isEvenLevel ? int.MinValue : int.MaxValue;
            for (var size = queue.Count - 1; size >= 0; --size) {
                var currentNode = queue.Dequeue();

                if (isEvenLevel) {
                    if (IsEven(currentNode.val) || previousValue >= currentNode.val) {
                        return false;
                    }
                } else {
                    if (!IsEven(currentNode.val) || previousValue <= currentNode.val) {
                        return false;
                    }
                }
                if (currentNode.left != null) {
                    queue.Enqueue(currentNode.left);
                }
                if (currentNode.right != null) {
                    queue.Enqueue(currentNode.right);
                }
                previousValue = currentNode.val;
            }
            isEvenLevel = !isEvenLevel;
        }
        return true;
    }

    private bool IsEven(int value) {
        return value % 2 == 0;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Mar 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to determine an even odd tree
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public bool IsEvenOddTree(TreeNode root) {
        var queue = new Queue<TreeNode>();
        queue.Enqueue(root);
 
        var isEvenLevel = true;
        while (queue.Count > 0) {
            int previousValue = isEvenLevel ? int.MinValue : int.MaxValue;
            for (var size = queue.Count - 1; size >= 0; --size) {
                var currentNode = queue.Dequeue();
 
                if (isEvenLevel) {
                    if (IsEven(currentNode.val) || previousValue >= currentNode.val) {
                        return false;
                    }
                } else {
                    if (!IsEven(currentNode.val) || previousValue <= currentNode.val) {
                        return false;
                    }
                }
                if (currentNode.left != null) {
                    queue.Enqueue(currentNode.left);
                }
                if (currentNode.right != null) {
                    queue.Enqueue(currentNode.right);
                }
                previousValue = currentNode.val;
            }
            isEvenLevel = !isEvenLevel;
        }
        return true;
    }
 
    private bool IsEven(int value) {
        return value % 2 == 0;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

true false false

C# || How To Group People Given The Group Size They Belong To Using C#

February 14, 2024 admin No comments

The following is a module with functions which demonstrates how to group people given the group size they belong to using C#.

1. Group The People – Problem Statement

There are n people that are split into some unknown number of groups. Each person is labeled with a unique ID from 0 to n – 1.

You are given an integer array groupSizes, where groupSizes[i] is the size of the group that person i is in. For example, if groupSizes[1] = 3, then person 1 must be in a group of size 3.

Return a list of groups such that each person i is in a group of size groupSizes[i].

Each person should appear in exactly one group, and every person must be in a group. If there are multiple answers, return any of them. It is guaranteed that there will be at least one valid solution for the given input.

Example 1:

Input: groupSizes = [3,3,3,3,3,1,3] Output: [[5],[0,1,2],[3,4,6]] Explanation: The first group is [5]. The size is 1, and groupSizes[5] = 1. The second group is [0,1,2]. The size is 3, and groupSizes[0] = groupSizes[1] = groupSizes[2] = 3. The third group is [3,4,6]. The size is 3, and groupSizes[3] = groupSizes[4] = groupSizes[6] = 3. Other possible solutions are [[2,1,6],[5],[0,4,3]] and [[5],[0,6,2],[4,3,1]].

Example 2:

Input: groupSizes = [2,1,3,3,3,2] Output: [[1],[0,5],[2,3,4]]

2. Group The People – Solution

The following is a solution which demonstrates how to group people given the group size they belong to.





		
		
			2. Group The People - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Feb 14, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to group people given group they belong to
// ============================================================================
public class Solution {
    public IList<IList<int>> GroupThePeople(int[] groupSizes) {
        var ans = new List<IList<int>>();

        // A map from group size to the list of indices that are there in the group.
        var szToGroup = new Dictionary<int, List<int>>();
        for (int i = 0; i < groupSizes.Length; i++) {
            if (!szToGroup.ContainsKey(groupSizes[i])) {
                szToGroup.Add(groupSizes[i], new List<int>());
            }

            var group = szToGroup[groupSizes[i]];
            group.Add(i);

            // When the list size equals the group size, empty it and store it in the answer.
            if (group.Count == groupSizes[i]) {
                ans.Add(group);
                szToGroup.Remove(groupSizes[i]);
            }
        }

        return ans;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Feb 14, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to group people given group they belong to
// ============================================================================
public class Solution {
    public IList<IList<int>> GroupThePeople(int[] groupSizes) {
        var ans = new List<IList<int>>();
 
        // A map from group size to the list of indices that are there in the group.
        var szToGroup = new Dictionary<int, List<int>>();
        for (int i = 0; i < groupSizes.Length; i++) {
            if (!szToGroup.ContainsKey(groupSizes[i])) {
                szToGroup.Add(groupSizes[i], new List<int>());
            }
 
            var group = szToGroup[groupSizes[i]];
            group.Add(i);
 
            // When the list size equals the group size, empty it and store it in the answer.
            if (group.Count == groupSizes[i]) {
                ans.Add(group);
                szToGroup.Remove(groupSizes[i]);
            }
        }
 
        return ans;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[[0,1,2],[5],[3,4,6]] [[1],[2,3,4],[0,5]]

C# || How To Find Minimum Deletions To Make Character Frequencies Unique Using C#

February 01, 2024 admin No comments

The following is a module with functions which demonstrates how to find the minimum deletions to make character frequencies unique using C#.

1. Min Deletions – Problem Statement

A string s is called good if there are no two different characters in s that have the same frequency.

Given a string s, return the minimum number of characters you need to delete to make s good.

The frequency of a character in a string is the number of times it appears in the string. For example, in the string “aab”, the frequency of ‘a’ is 2, while the frequency of ‘b’ is 1.

Example 1:

Input: s = "aab" Output: 0 Explanation: s is already good.

Example 2:

Input: s = "aaabbbcc" Output: 2 Explanation: You can delete two 'b's resulting in the good string "aaabcc". Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc".

Example 3:

Input: s = "ceabaacb" Output: 2 Explanation: You can delete both 'c's resulting in the good string "eabaab". Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).

2. Min Deletions – Solution

The following is a solution which demonstrates how to find the minimum deletions to make character frequencies unique.





		
		
			2. Min Operations - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Feb 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find minimum deletions to make unique
// ============================================================================
public class Solution {
    public int MinDeletions(string s) {
        // Store the frequency of each character
        int[] frequency = new int[26];
        for (int i = 0; i < s.Length; i++) {
            frequency[s[i] - 'a']++;
        }

        Array.Sort(frequency);

        int deleteCount = 0;
        // Maximum frequency the current character can have
        int maxFreqAllowed = s.Length;

        // Iterate over the frequencies in descending order
        for (int i = 25; i >= 0 && frequency[i] > 0; i--) {
            // Delete characters to make the frequency equal the maximum frequency allowed
            if (frequency[i] > maxFreqAllowed) {
                deleteCount += frequency[i] - maxFreqAllowed;
                frequency[i] = maxFreqAllowed;
            }
            // Update the maximum allowed frequency
            maxFreqAllowed = Math.Max(0, frequency[i] - 1);
        }

        return deleteCount;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Feb 1, 2024
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find minimum deletions to make unique
// ============================================================================
public class Solution {
    public int MinDeletions(string s) {
        // Store the frequency of each character
        int[] frequency = new int[26];
        for (int i = 0; i < s.Length; i++) {
            frequency[s[i] - 'a']++;
        }
 
        Array.Sort(frequency);
 
        int deleteCount = 0;
        // Maximum frequency the current character can have
        int maxFreqAllowed = s.Length;
 
        // Iterate over the frequencies in descending order
        for (int i = 25; i >= 0 && frequency[i] > 0; i--) {
            // Delete characters to make the frequency equal the maximum frequency allowed
            if (frequency[i] > maxFreqAllowed) {
                deleteCount += frequency[i] - maxFreqAllowed;
                frequency[i] = maxFreqAllowed;
            }
            // Update the maximum allowed frequency
            maxFreqAllowed = Math.Max(0, frequency[i] - 1);
        }
 
        return deleteCount;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

0 2 2

Tag Archives: c-sharp

C# || How To Split Linked List In Parts Using C#

C# || How To Get First X Rows of Pascal’s Triangle Using C#

C# || How To Get Smallest String Starting From Leaf Using C#

C# || How To Convert Integer To English Words Using C#

C# || How To Find Mode In Binary Search Tree Using C#

C# || How To Find The Winner Of Array Game Using C#

C# || How To Design Seat Reservation Manager Using C#

C# || How To Restore Array From Adjacent Pairs Using C#

C# || How To Design Graph With Shortest Path Calculator Using C#

C# || How To Find Largest 3 Same Digit Number In String Using C#

C# || How To Find Largest Odd Number In String Using C#

C# || How To Determine If A Binary Tree Is Even Odd Tree Using C#

C# || How To Group People Given The Group Size They Belong To Using C#

C# || How To Find Minimum Deletions To Make Character Frequencies Unique Using C#

Search

Compile Your Code Now

Translate Page

Popular Pages

Recent

Archives

Categories