Tag Archives: c-sharp
C# || How To Find Minimum In Rotated Sorted Array With Duplicates Using C#

The following is a module with functions which demonstrates how to find the minimum value in a rotated sorted array with duplicates using C#.
1. Find Min Duplicates – Problem Statement
Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,4,4,5,6,7] might become:
- [4,5,6,7,0,1,4] if it was rotated 4 times.
- [0,1,4,4,5,6,7] if it was rotated 7 times.
Notice that rotating an array [a[0], a[1], a[2], …, a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], …, a[n-2]].
Given the sorted rotated array nums that may contain duplicates, return the minimum element of this array.
You must decrease the overall operation steps as much as possible.
Example 1:
Input: nums = [1,3,5]
Output: 1
Example 2:
Input: nums = [2,2,2,0,1]
Output: 0
2. Find Min Duplicates – Solution
The following is a solution which demonstrates how to find the minimum value in a rotated sorted array with duplicates.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 22, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to find the minimum value in a sorted array // ============================================================================ public class Solution { public int FindMin(int[] nums) { var lo = 0; var hi = nums.Length - 1; // In cases where the front and back of the array are the // same (ex: [1,19,28,87,91,0,1,1,1]), decrease the end of the array while (nums[lo] == nums[hi] && lo < hi) { --hi; } // Perform binary search while (lo < hi) { var mid = lo + (hi - lo) / 2; // Midpoint element is greater than right side of array, so // the minumum element is somewhere on the right side of array. // Advance lo value to equal midpoint + 1 if (nums[mid] > nums[hi]) { lo = mid + 1; // Midpoint element is less than right side of array, so // the minumum element is somewhere on the left side of array. // Decrease hi value to equal midpoint } else if (nums[mid] < nums[hi]) { hi = mid; // Duplicate element found (nums[mid] == nums[hi]) } else { --hi; } } return nums[lo]; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
1
0
C# || How To Find Minimum In Rotated Sorted Array Using C#

The following is a module with functions which demonstrates how to find the minimum value in a rotated sorted array using C#.
1. Find Min – Problem Statement
Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:
- [4,5,6,7,0,1,2] if it was rotated 4 times.
- [0,1,2,4,5,6,7] if it was rotated 7 times.
Notice that rotating an array [a[0], a[1], a[2], …, a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], …, a[n-2]].
Given the sorted rotated array nums of unique elements, return the minimum element of this array.
You must write an algorithm that runs in O(log n) time.
Example 1:
Input: nums = [3,4,5,1,2]
Output: 1
Explanation: The original array was [1,2,3,4,5] rotated 3 times.
Example 2:
Input: nums = [4,5,6,7,0,1,2]
Output: 0
Explanation: The original array was [0,1,2,4,5,6,7] and it was rotated 4 times.
Example 3:
Input: nums = [11,13,15,17]
Output: 11
Explanation: The original array was [11,13,15,17] and it was rotated 4 times.
2. Find Min – Solution
The following is a solution which demonstrates how to find the minimum value in a rotated sorted array.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 22, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to find the minimum value in a sorted array // ============================================================================ public class Solution { public int FindMin(int[] nums) { var lo = 0; var hi = nums.Length - 1; while (lo < hi) { var mid = lo + (hi - lo) / 2; // Midpoint element is greater than right side of array, so // the minumum element is somewhere on the right side of array. // Advance lo value to equal midpoint + 1 if (nums[mid] > nums[hi]) { lo = mid + 1; // Midpoint element is less than right side of array, so // the minumum element is somewhere on the left side of array. // Decrease hi value to equal midpoint } else if (nums[mid] < nums[hi]) { hi = mid; // Minimum element found } else { lo = mid; break; } } return nums[lo]; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
1
0
11
C# || How To Find Longest Arithmetic Subsequence Of An Array Using C#

The following is a module with functions which demonstrates how to find the longest arithmetic subsequence of an array using C#.
1. Longest Arithmetic Subsequence Length – Problem Statement
Given an array nums of integers, return the length of the longest arithmetic subsequence in nums.
Recall that a subsequence of an array nums is a list nums[i1], nums[i2], …, nums[ik] with 0 <= i1 < i2 < … < ik <= nums.length – 1, and that a sequence seq is arithmetic if seq[i+1] – seq[i] are all the same value (for 0 <= i < seq.length – 1).
Example 1:
Input: nums = [3,6,9,12]
Output: 4
Explanation:
The whole array is an arithmetic sequence with steps of length = 3.
Example 2:
Input: nums = [9,4,7,2,10]
Output: 3
Explanation:
The longest arithmetic subsequence is [4,7,10].
Example 3:
Input: nums = [20,1,15,3,10,5,8]
Output: 4
Explanation:
The longest arithmetic subsequence is [20,15,10,5].
2. Longest Arithmetic Subsequence Length – Solution
The following is a solution which demonstrates how to find the longest arithmetic subsequence of an array.
The main idea in this solution is to maintain a dictionary map array of the differences seen at each index, where dp[index][diff] holds the frequency count at that index, for that specific diff.
Each item in the array is considered and checked against to their items to the left.
For each number (i,j) we determine the difference d = nums[i] – nums[j] and keep a count of the frequency the difference has been seen.
In the end, the max difference frequency is returned.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 22, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to find longest arithmetic subsequence // ============================================================================ public class Solution { public int LongestArithSeqLength(int[] nums) { var result = 0; // Create a map array of size n var dp = new Dictionary<int, int>[nums.Length]; // Iterate the numbers in the array for (int i = 0; i < nums.Length; ++i) { // Create a new dictionary for this index dp[i] = new Dictionary<int, int>(); // Iterate over values to the left of i for (int j = 0; j < i; ++j) { // Get the difference between the two numbers var currentDiff = nums[i] - nums[j]; // Update the count matching the difference already seen from j for i dp[i][currentDiff] = (dp[j].ContainsKey(currentDiff) ? dp[j][currentDiff] : 0) + 1; // Keep track of the max difference count result = Math.Max(result, dp[i][currentDiff]); } } return result + 1; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
4
3
4
C# || How To Implement RandomizedCollection – Insert Delete GetRandom O(1) Duplicates Allowed Using C#

The following is a module with functions which demonstrates how to implement RandomizedCollection – Insert Delete GetRandom O(1) Duplicates Allowed using C#.
1. RandomizedCollection – Problem Statement
Implement the RandomizedCollection class:
- RandomizedCollection() Initializes the RandomizedCollection object.
- bool insert(int val) Inserts an item val into the multiset if not present. Returns true if the item was not present, false otherwise.
- bool remove(int val) Removes an item val from the multiset if present. Returns true if the item was present, false otherwise. Note that if val has multiple occurrences in the multiset, we only remove one of them.
- int getRandom() Returns a random element from the current multiset of elements (it’s guaranteed that at least one element exists when this method is called). The probability of each element being returned is linearly related to the number of same values the multiset contains.
You must implement the functions of the class such that each function works in average O(1) time complexity.
Example 1:
Input
Input
["RandomizedCollection", "insert", "insert", "insert", "getRandom", "remove", "getRandom"]
[[], [1], [1], [2], [], [1], []]
Output
[null, true, false, true, 2, true, 1]Explanation
RandomizedCollection randomizedCollection = new RandomizedCollection();
randomizedCollection.insert(1); // return True. Inserts 1 to the collection. Returns true as the collection did not contain 1.
randomizedCollection.insert(1); // return False. Inserts another 1 to the collection. Returns false as the collection contained 1. Collection now contains [1,1].
randomizedCollection.insert(2); // return True. Inserts 2 to the collection, returns true. Collection now contains [1,1,2].
randomizedCollection.getRandom(); // getRandom should return 1 with the probability 2/3, and returns 2 with the probability 1/3.
randomizedCollection.remove(1); // return True. Removes 1 from the collection, returns true. Collection now contains [1,2].
randomizedCollection.getRandom(); // getRandom should return 1 and 2 both equally likely.
2. RandomizedCollection – Solution
The following is a solution which demonstrates how to implement RandomizedCollection – Insert Delete GetRandom O(1) Duplicates Allowed.
The main idea of this solution is to use a list to store the values added, and use a map to determine if an item has been added already.
The map is also used to store the list index of the added item. This makes it so we know which index to work with when we want to remove an item from the list. The indexes of the added items are stored using a set.
To ensure proper removal, we ‘swap’ places of the value to remove with the last item in the list. This makes it so only the last item in the list is always the index to have items removed from.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 21, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to implement RandomizedCollection // ============================================================================ public class RandomizedCollection { // For randomizing the list private Random r; // To determine if an item has been added, and store its list index private Dictionary<int, HashSet<int>> map; // To store the items added private List<int> values; public RandomizedCollection() { r = new Random(); map = new Dictionary<int, HashSet<int>>(); values = new List<int>(); } // Inserts a value to the set. Returns true if the set did not already contain the specified element public bool Insert(int val) { var result = false; // Determine if item exists in map if (!map.ContainsKey(val)) { map[val] = new HashSet<int>(); result = true; } // Add value to the list values.Add(val); // Save the value with its list index to the set map[val].Add(values.Count - 1); return result; } // Removes a value from the set. Returns true if the set contained the specified element public bool Remove(int val) { // Determine if item exists in map if (!map.ContainsKey(val)) { return false; } // Get the last item index var lastItemIndex = values.Count - 1; // Get the first index in the set. // This the current index for the item to remove var itemToRemoveIndex = map[val].First(); // Remove this index from the set map[val].Remove(itemToRemoveIndex); // 'Swap' places of the last item in the list with the item to remove if (itemToRemoveIndex != lastItemIndex) { // Get the last index for the item at the end var needToModifyItem = values[lastItemIndex]; // 'Swap' places of the last item in the list with the item to be removed values[itemToRemoveIndex] = needToModifyItem; // Remove the previous index and add its new index map[needToModifyItem].Add(itemToRemoveIndex); map[needToModifyItem].Remove(lastItemIndex); } // Remove the previous index from the list values.RemoveAt(lastItemIndex); // Remove the value from the map if there are no more entries in the set if (map[val].Count == 0) { map.Remove(val); } return true; } // Get a random element from the set public int GetRandom() { var randomIndex = r.Next(0, values.Count); return values[randomIndex]; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[null,true,false,true,2,true,2]
C# || How To Implement RandomizedSet – Insert Delete GetRandom O(1) Using C#

The following is a module with functions which demonstrates how to implement RandomizedSet – Insert Delete GetRandom O(1) using C#.
1. RandomizedSet – Problem Statement
Implement the RandomizedSet class:
- RandomizedSet() Initializes the RandomizedSet object.
- bool insert(int val) Inserts an item val into the set if not present. Returns true if the item was not present, false otherwise.
- bool remove(int val) Removes an item val from the set if present. Returns true if the item was present, false otherwise.
- int getRandom() Returns a random element from the current set of elements (it’s guaranteed that at least one element exists when this method is called). Each element must have the same probability of being returned.
You must implement the functions of the class such that each function works in average O(1) time complexity.
Example 1:
Input
["RandomizedSet", "insert", "remove", "insert", "getRandom", "remove", "insert", "getRandom"]
[[], [1], [2], [2], [], [1], [2], []]
Output
[null, true, false, true, 2, true, false, 2]Explanation
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // Inserts 1 to the set. Returns true as 1 was inserted successfully.
randomizedSet.remove(2); // Returns false as 2 does not exist in the set.
randomizedSet.insert(2); // Inserts 2 to the set, returns true. Set now contains [1,2].
randomizedSet.getRandom(); // getRandom() should return either 1 or 2 randomly.
randomizedSet.remove(1); // Removes 1 from the set, returns true. Set now contains [2].
randomizedSet.insert(2); // 2 was already in the set, so return false.
randomizedSet.getRandom(); // Since 2 is the only number in the set, getRandom() will always return 2.
2. RandomizedSet – Solution
The following is a solution which demonstrates how to implement RandomizedSet – Insert Delete GetRandom O(1).
The main idea of this solution is to use a list to store the values added, and use a map to determine if an item has been added already.
The map is also used to store the list index of the added item. This makes it so we know which index to work with when we want to remove an item from the list.
To ensure proper removal, we ‘swap’ places of the value to remove with the last item in the list. This makes it so only the last item in the list is always the index to have items removed from.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 20, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to implement RandomizedSet // ============================================================================ public class RandomizedSet { // For randomizing the list private Random r; // To determine if an item has been added, and store its list index private Dictionary<int, int> map; // To store the items added private List<int> values; public RandomizedSet() { r = new Random(); map = new Dictionary<int, int>(); values = new List<int>(); } // Inserts a value to the set. Returns true if the set did not already contain the specified element public bool Insert(int val) { // Determine if item exists in map if (map.ContainsKey(val)) { return false; } // Add value to the list values.Add(val); // Save the value with its list index to the map map[val] = values.Count - 1; return true; } // Removes a value from the set. Returns true if the set contained the specified element public bool Remove(int val) { // Determine if item exists in map if (!map.ContainsKey(val)) { return false; } // Get the current index for the item to remove var currentIndex = map[val]; // Get the last index for the item at the end var lastIndex = values.Count - 1; // 'Swap' places of the last item in the list with the item to be removed values[currentIndex] = values[lastIndex]; // Update the map for the item that we 'swapped' with its new list index map[values[currentIndex]] = currentIndex; // Remove the swapped item from the list (this is the item to be removed) values.RemoveAt(lastIndex); // Remove the item to be removed from the map map.Remove(val); return true; } // Get a random element from the set public int GetRandom() { var randomIndex = r.Next(0, values.Count); return values[randomIndex]; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[null,true,false,true,1,true,false,2]
C# || How To Determine Whether A Binary Tree Is A Symmetric Tree Using C#

The following is a module with functions which demonstrates how to determine whether a binary tree is a symmetric tree using C#.
1. Is Symmetric – Problem Statement
Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Example 1:
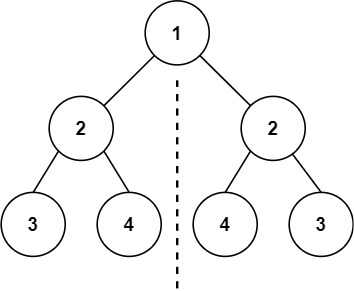
Input: root = [1,2,2,3,4,4,3]
Output: true
Example 2:
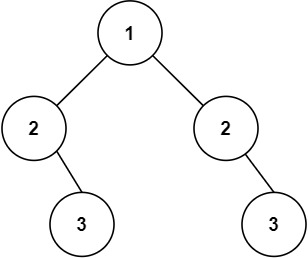
Input: root = [1,2,2,null,3,null,3]
Output: false
2. Is Symmetric – Solution
The following is a solution which demonstrates how to determine whether a binary tree is a symmetric tree.
For two trees to be mirror images, the following three conditions must be true:
• 1 - Their root node's key must be same
• 2 - The left subtree of left tree and right subtree of right tree have to be mirror images
• 3 - The right subtree of left tree and left subtree of right tree have to be mirror images
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 20, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Determines whether a binary tree is a symmetric tree // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { public bool IsSymmetric(TreeNode root) { return IsMirror(root, root); } private bool IsMirror(TreeNode a, TreeNode b) { if (a == null && b == null) { return true; } if (a == null || b == null) { return false; } // 1. The two root nodes have the same value // 2. The left subtree of one root node is a mirror // reflection of the right subtree of the other root node // 3. The right subtree of one root node is a mirror // reflection of the left subtree of the other root node return a.val == b.val && IsMirror(a.left, b.right) && IsMirror(a.right, b.left); } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
true
false
C# || How To Traverse Bottom Up Binary Tree Level Order Using C#

The following is a module with functions which demonstrates how to traverse bottom up binary tree level order using C#.
1. Level Order Bottom – Problem Statement
Given the root of a binary tree, return the bottom-up level order traversal of its nodes’ values. (i.e., from left to right, level by level from leaf to root).
Example 1:
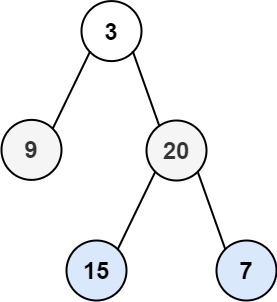
Input: root = [3,9,20,null,null,15,7]
Output: [[15,7],[9,20],[3]]
Example 2:
Input: root = [1]
Output: [[1]]
Example 3:
Input: root = []
Output: []
2. Level Order Bottom – Solution
The following is a solution which demonstrates how to traverse bottom up binary tree level order.
The idea of this solution is to have a result list which keeps track of the items found on each level. A variable is also used to keep track of the maximum depth levels in the tree. The max depth level is used to insert node values into their appropriate result list slot.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 20, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Determines how to traverse a tree bottom up level order // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { private List<IList<int>> result = new List<IList<int>>(); private int maxDepth = 0; public IList<IList<int>> LevelOrderBottom(TreeNode root) { Traverse(root, 0); return result; } private void Traverse(TreeNode node, int depth) { if (node == null) { return; } // Keep track of max depth level if (depth > maxDepth) { maxDepth = depth; } // Determine if new depth level should be added to the result list // Add the new level to the start of the result list if (result.Count == depth) { result.Insert(0, new List<int>()); } // Add the current node value to the corresponding result level index result[maxDepth - depth].Add(node.val); // Keep exploring left and right nodes Traverse(node.left, depth + 1); Traverse(node.right, depth + 1); } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[[15,7],[9,20],[3]]
[[1]]
[]
C# || How To Get The Sum Of Binary Tree Nodes With Even Valued Grandparents Using C#

The following is a module with functions which demonstrates how to get the sum of binary tree nodes with even valued grandparents using C#.
1. Sum Even Grandparent – Problem Statement
Given the root of a binary tree, return the sum of values of nodes with an even-valued grandparent. If there are no nodes with an even-valued grandparent, return 0.
A grandparent of a node is the parent of its parent if it exists.
Example 1:
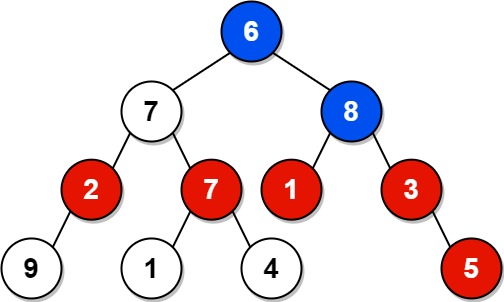
Input: root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
Output: 18
Explanation: The red nodes are the nodes with even-value grandparent while the blue nodes are the even-value grandparents.
Example 2:

Input: root = [1]
Output: 0
2. Sum Even Grandparent – Solution
The following is a solution which demonstrates how to get the sum of binary tree nodes with even valued grandparents.
The idea of this solution is to simply traverse the tree, and for each recursive call, we keep track of the parent node and the grandparent node of each node.
If a node has a grandparent, we check to see if it is an even number. If it is, the result is incremented.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 20, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Determines how to get the sum of even valued tree grandparents // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { private int result = 0; public int SumEvenGrandparent(TreeNode root) { Traverse(root, null, null); return result; } private void Traverse(TreeNode node, TreeNode parent, TreeNode grandParent) { if (node == null) { return; } // If a grandparent exists and its an even number, // add the current node value to the result if (grandParent != null && grandParent.val % 2 == 0) { result += node.val; } // Keep exploring left & right nodes // setting the current node as the parent // and the current parent node as the grandparent Traverse(node.left, node, parent); Traverse(node.right, node, parent); } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
18
0
C# || How To Get The Number Of Binary Tree Paths Equal To Path Sum Using C#

The following is a module with functions which demonstrates how to get the number of binary tree paths equal to path sum using C#.
1. Number Of Path Sum Paths – Problem Statement
Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.
The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).
Example 1:
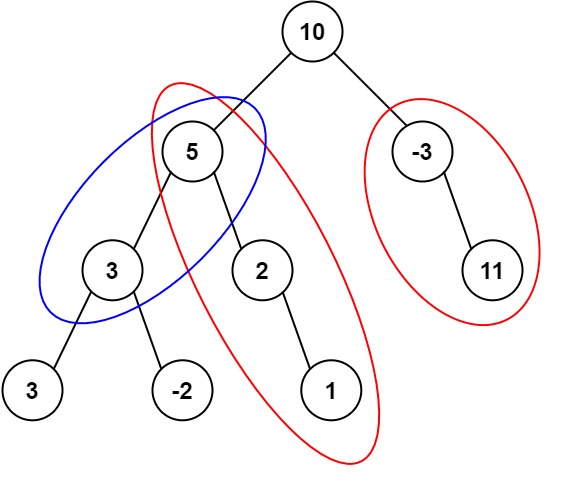
Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output: 3
Explanation: The paths that sum to 8 are shown.
Example 2:
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: 3
2. Number Of Path Sum Paths – Solution
The following is a solution which demonstrates how to get the number of binary tree paths equal to path sum.
The main idea here is that the sum at each level for each path is calculated. When the next level is explored, the value at the previous level is summed together with the node value at the current level.
A map dictionary is used to keep track of the sum at each level. If the prefix sum at the previous level is enough to equal the target path sum at the current level, the result count is incremented.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 18, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Determines how to get the number of tree paths equal to path sum // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { private int result = 0; private Dictionary<int, int> sumFrequency = new Dictionary<int, int>(); public int PathSum(TreeNode root, int targetSum) { sumFrequency[0] = 1; Search(root, targetSum, 0); return result; } public void Search(TreeNode node, int targetSum, int currentSum) { if (node == null) { return; } // Determine the current sum currentSum = currentSum + node.val; // Get the path prefix sum var prefixSum = currentSum - targetSum; if (sumFrequency.ContainsKey(prefixSum)) { result += sumFrequency[prefixSum]; } // Increment the number of times this prefix has been seen sumFrequency[currentSum] = (sumFrequency.ContainsKey(currentSum) ? sumFrequency[currentSum] : 0) + 1; // Keep exploring along branches finding the target sum Search(node.left, targetSum, currentSum); Search(node.right, targetSum, currentSum); // Remove value of this prefixSum (path's been explored) --sumFrequency[currentSum]; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
3
3
C# || How To Get All Root To Leaf Binary Tree Paths Equal To Path Sum Using C#

The following is a module with functions which demonstrates how to get all the root to leaf binary tree paths equal to path sum using C#.
1. Root To Leaf Path Sum – Problem Statement
Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where the sum of the node values in the path equals targetSum. Each path should be returned as a list of the node values, not node references.
A root-to-leaf path is a path starting from the root and ending at any leaf node. A leaf is a node with no children.
Example 1:
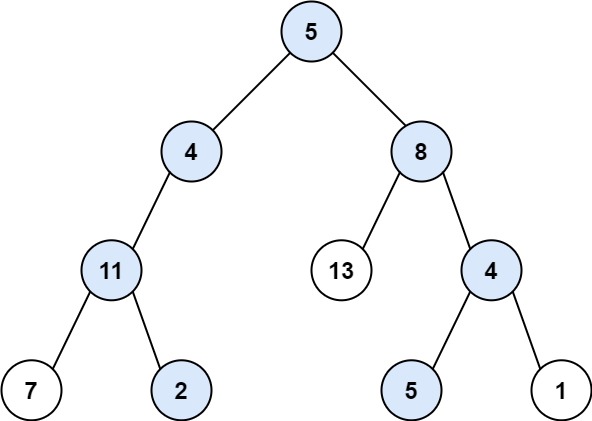
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2],[5,8,4,5]]
Explanation: There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
Example 2:
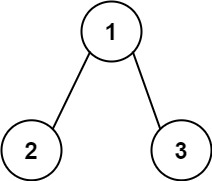
Input: root = [1,2,3], targetSum = 5
Output: []
Example 3:
Input: root = [1,2], targetSum = 0
Output: []
2. Root To Leaf Path Sum – Solution
The following is a solution which demonstrates how to get all the root to leaf binary tree paths equal to path sum.
The main idea here is that the sum at each level for each path is calculated until we reach the end of the root-to-leaf.
A list is used to store the node value at each level. When the next level is explored, the value is appended to the list, and the process continues.
When we reach the end of the leaf, we check to see if the target value has been reached. If so, we add the node values that make up the path to the result list.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 18, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Determines how to get all root to leaf path sum in a tree // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { private List<IList<int>> result = new List<IList<int>>(); public IList<IList<int>> PathSum(TreeNode root, int targetSum) { Search(root, targetSum, 0, new List<int>()); return result; } private void Search(TreeNode node, int targetSum, int currentSum, List<int> path) { if (node == null) { return; } // Add the node to this path path.Add(node.val); // Add the current value to the running total currentSum = currentSum + node.val; // Since this is a root-to-leaf check, evaluate for the // success condition when both left and right nodes are null if (node.left == null && node.right == null) { // Check to see if current value equals target if (currentSum == targetSum) { result.Add(new List<int>(path)); } } // Keep exploring along branches finding the target sum Search(node.left, targetSum, currentSum, path); Search(node.right, targetSum, currentSum, path); // Remove the last item added as this path has already been explored path.RemoveAt(path.Count - 1); } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[[5,4,11,2],[5,8,4,5]]
[]
[]
C# || How To Determine If Binary Tree Root To Leaf Path Sum Exists Using C#

The following is a module with functions which demonstrates how to determine if a binary tree root to leaf path sum exists using C#.
1. Has Path Sum – Problem Statement
Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.
A leaf is a node with no children.
Example 1:
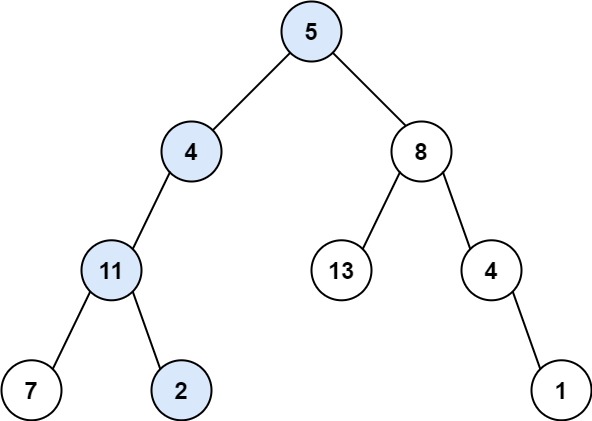
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
Example 2:

Input: root = [1,2,3], targetSum = 5
Output: false
Example 3:
Input: root = [1,2], targetSum = 0
Output: false
2. Has Path Sum – Solution
The following is a solution which demonstrates how to determine if a binary tree root to leaf path sum exists.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 18, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Determines if a root to leaf path sum exists in a binary tree // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { public bool HasPathSum(TreeNode root, int targetSum) { return Search(root, targetSum); } public bool Search(TreeNode node, int targetSum) { if (node == null) { return false; } // Determine the current sum targetSum = targetSum - node.val; // Since this is a root-to-leaf check, evaluate for the // success condition when both left and right nodes are null if (node.left == null && node.right == null) { return targetSum == 0; } // Keep exploring along branches finding the target sum return Search(node.left, targetSum) || Search(node.right, targetSum); } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
true
false
false
C# || How To Convert Sorted Array To Binary Search Tree Using C#

The following is a module with functions which demonstrates how to convert a sorted array to a binary search tree using C#.
1. Sorted Array To BST – Problem Statement
Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.
A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.
Example 1:
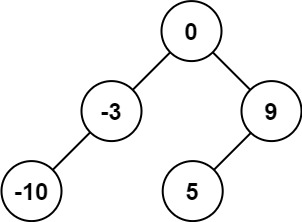
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted:

Example 2:
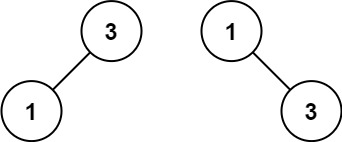
Input: nums = [1,3]
Output: [3,1]
Explanation: [1,3] and [3,1] are both a height-balanced BSTs.
2. Sorted Array To BST – Solution
The following is a solution which demonstrates how to convert a sorted array to a binary search tree.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 18, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to convert sorted array to BST // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { public TreeNode SortedArrayToBST(int[] nums) { return BuildBST(nums, 0, nums.Length -1); } TreeNode BuildBST(int[] nums, int start, int end) { if (start > end) { return null; } var mid = start + (end - start) / 2; var node = new TreeNode(nums[mid]); node.left = BuildBST(nums, start, mid - 1); node.right = BuildBST(nums, mid + 1, end); return node; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[0,-10,5,null,-3,null,9]
[1,null,3]
C# || How To Convert 1D Array Into 2D Array Using C#

The following is a module with functions which demonstrates how to convert a 1D array into a 2D array using C#.
1. Construct 2D Array – Problem Statement
You are given a 0-indexed 1-dimensional (1D) integer array original, and two integers, m and n. You are tasked with creating a 2-dimensional (2D) array with m rows and n columns using all the elements from original.
The elements from indices 0 to n – 1 (inclusive) of original should form the first row of the constructed 2D array, the elements from indices n to 2 * n – 1 (inclusive) should form the second row of the constructed 2D array, and so on.
Return an m x n 2D array constructed according to the above procedure, or an empty 2D array if it is impossible.
Example 1:
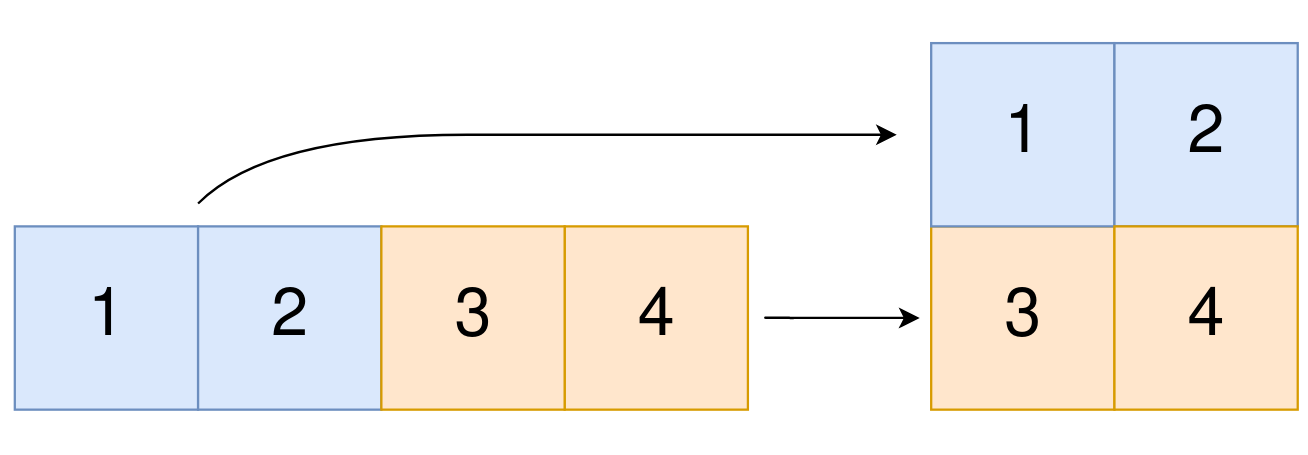
Input: original = [1,2,3,4], m = 2, n = 2
Output: [[1,2],[3,4]]
Explanation:
The constructed 2D array should contain 2 rows and 2 columns.
The first group of n=2 elements in original, [1,2], becomes the first row in the constructed 2D array.
The second group of n=2 elements in original, [3,4], becomes the second row in the constructed 2D array.
Example 2:
Input: original = [1,2,3], m = 1, n = 3
Output: [[1,2,3]]
Explanation:
The constructed 2D array should contain 1 row and 3 columns.
Put all three elements in original into the first row of the constructed 2D array.
Example 3:
Input: original = [1,2], m = 1, n = 1
Output: []
Explanation:
There are 2 elements in original.
It is impossible to fit 2 elements in a 1x1 2D array, so return an empty 2D array.
Example 4:
Input: original = [3], m = 1, n = 2
Output: []
Explanation:
There is 1 element in original.
It is impossible to make 1 element fill all the spots in a 1x2 2D array, so return an empty 2D array.
2. Construct 2D Array – Solution
The following is a solution which demonstrates how to convert a 1D array into a 2D array.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 18, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Demonstrates how to convert a 1D array into a 2D array // ============================================================================ public class Solution { public int[][] Construct2DArray(int[] original, int m, int n) { // Determine if parameters are valid if (original.Length != m * n) { return new int[0][]; } // Create 2D array var result = new int[m][]; for (int row = 0; row < result.Length; ++row) { result[row] = new int[n]; } // Populate result for (int index = 0; index < original.Length; ++index) { // Determine the result array row and column index var rowIndex = index / n; var colIndex = index % n; // Copy values to result result[rowIndex][colIndex] = original[index]; } return result; } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
[[1,2],[3,4]]
[[1,2,3]]
[]
[]
C# || How To Find Cousins In A Binary Tree Using C#

The following is a module with functions which demonstrates how to find the cousins in a binary tree using C#.
1. Is Cousins – Problem Statement
Given the root of a binary tree with unique values and the values of two different nodes of the tree x and y, return true if the nodes corresponding to the values x and y in the tree are cousins, or false otherwise.
Two nodes of a binary tree are cousins if they have the same depth with different parents.
Note that in a binary tree, the root node is at the depth 0, and children of each depth k node are at the depth k + 1.
Example 1:

Input: root = [1,2,3,4], x = 4, y = 3
Output: false
Example 2:

Input: root = [1,2,3,null,4,null,5], x = 5, y = 4
Output: true
Example 3:

Input: root = [1,2,3,null,4], x = 2, y = 3
Output: false
2. Is Cousins – Solution
The following is a solution which demonstrates how to determine if x and y values are cousins in a binary tree.
The idea here is to explore each path, finding the node values that represent x and y.
Once both values are found, save the depth and parent node, and determine if they are cousins
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
// ============================================================================ // Author: Kenneth Perkins // Date: Oct 17, 2021 // Taken From: http://programmingnotes.org/ // File: Solution.cs // Description: Determines if x and y are cousins in a binary tree // ============================================================================ /** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { // For the x parent and depth values private int xParent = -1; private int xDepth = -1; // For the y parent and depth values private int yParent = -1; private int yDepth = -1; public bool IsCousins(TreeNode root, int x, int y) { Search(root, x, y, root.val, 0); // Check for success condition return xParent != yParent && xDepth == yDepth; } private void Search(TreeNode node, int x, int y, int parent, int depth) { // Values have been found if (xParent != -1 && yParent != -1) { return; } if (node == null) { return; } if (node.val == x) { // Set the x parent and depth values xParent = parent; xDepth = depth; } else if (node.val == y) { // Set the y parent and depth values yParent = parent; yDepth = depth; } else { // Keep exploring along branches for the success condition Search(node.left, x, y, node.val, depth + 1); Search(node.right, x, y, node.val, depth + 1); } } }// http://programmingnotes.org/ |
QUICK NOTES:
The highlighted lines are sections of interest to look out for.
The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.
Once compiled, you should get this as your output for the example cases:
false
true
false












