dijkstra algorithm – My Programming Notes

Tag Archives: dijkstra algorithm

C# || How To Find The Cheapest Flights Within K Stops Using C#

April 01, 2023 admin No comments

The following is a module with functions which demonstrates how to find the cheapest flights within K stops using C#.

1. Find Cheapest Price – Problem Statement

There are n cities connected by some number of flights. You are given an array flights where flights[i] = [from_i, to_i, price_i] indicates that there is a flight from city from_i to city to_i with cost price_i.

You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.

Example 1:

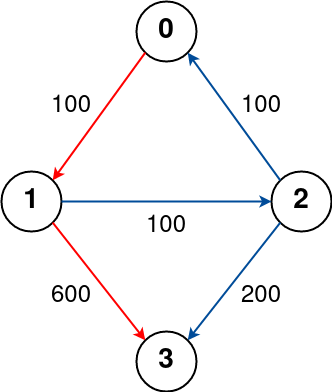
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1 Output: 700 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.

Example 2:

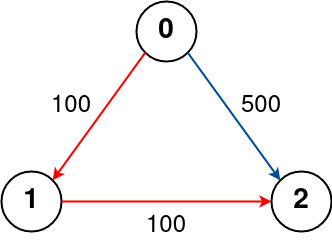
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.

Example 3:

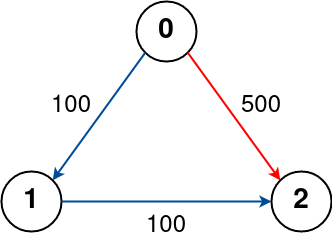
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown above. The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.

2. Find Cheapest Price – Solution

The following is a solution which demonstrates how to find the cheapest flights within K stops.





		
		
			2. Find Cheapest Price - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Apr 1, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find cheapest flights in k stops
// ============================================================================
public class Solution {
    public int FindCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        var adj = new Dictionary<int, List<int[]>>();
        foreach (int[] i in flights) {
            if (!adj.ContainsKey(i[0])) {
                adj[i[0]] = new List<int[]>();
            }
            adj[i[0]].Add(new int[] { i[1], i[2] });
        }

        int[] stops = new int[n];
        Array.Fill(stops, int.MaxValue);
        var pq = new PriorityQueue<int[], int[]>(Comparer<int[]>.Create((a, b) => a[0] - b[0]));

        // {dist_from_src_node, node, number_of_stops_from_src_node}
        var distance = new int[] { 0, src, 0 };
        pq.Enqueue(distance, distance);

        while (pq.Count > 0) {
            int[] temp = pq.Dequeue();
            int dist = temp[0];
            int node = temp[1];
            int steps = temp[2];
            // We have already encountered a path with a lower cost and fewer stops,
            // or the number of stops exceeds the limit.
            if (steps > stops[node] || steps > k + 1) {
                continue;
            }
            stops[node] = steps;
            if (node == dst) {
                return dist;
            }
            if (!adj.ContainsKey(node)) {
                continue;
            }
            foreach (int[] a in adj[node]) {
                var newDistance = new int[] { dist + a[1], a[0], steps + 1 };
                pq.Enqueue(newDistance, newDistance);
            }
        }
        return -1;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Apr 1, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find cheapest flights in k stops
// ============================================================================
public class Solution {
    public int FindCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        var adj = new Dictionary<int, List<int[]>>();
        foreach (int[] i in flights) {
            if (!adj.ContainsKey(i[0])) {
                adj[i[0]] = new List<int[]>();
            }
            adj[i[0]].Add(new int[] { i[1], i[2] });
        }
 
        int[] stops = new int[n];
        Array.Fill(stops, int.MaxValue);
        var pq = new PriorityQueue<int[], int[]>(Comparer<int[]>.Create((a, b) => a[0] - b[0]));
 
        // {dist_from_src_node, node, number_of_stops_from_src_node}
        var distance = new int[] { 0, src, 0 };
        pq.Enqueue(distance, distance);
 
        while (pq.Count > 0) {
            int[] temp = pq.Dequeue();
            int dist = temp[0];
            int node = temp[1];
            int steps = temp[2];
            // We have already encountered a path with a lower cost and fewer stops,
            // or the number of stops exceeds the limit.
            if (steps > stops[node] || steps > k + 1) {
                continue;
            }
            stops[node] = steps;
            if (node == dst) {
                return dist;
            }
            if (!adj.ContainsKey(node)) {
                continue;
            }
            foreach (int[] a in adj[node]) {
                var newDistance = new int[] { dist + a[1], a[0], steps + 1 };
                pq.Enqueue(newDistance, newDistance);
            }
        }
        return -1;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

700 200 500

Tag Archives: dijkstra algorithm

C# || How To Find The Cheapest Flights Within K Stops Using C#

Search

Compile Your Code Now

Translate Page

Popular Pages

Recent

Archives

Categories