leetcode – Page 6 – My Programming Notes

Tag Archives: leetcode

C# || How To Find The Largest Divisible Subset In Array Using C#

November 14, 2021 admin No comments

The following is a module with functions which demonstrates how to find the largest divisible subset in an array using C#.

1. Largest Divisible Subset – Problem Statement

Given a set of distinct positive integers nums, return the largest subset answer such that every pair (answer[i], answer[j]) of elements in this subset satisfies:

answer[i] % answer[j] == 0, or
answer[j] % answer[i] == 0

If there are multiple solutions, return any of them.

Example 1:

Input: nums = [1,2,3] Output: [1,2] Explanation: [1,3] is also accepted.

Example 2:

Input: nums = [1,2,4,8] Output: [1,2,4,8]

2. Largest Divisible Subset – Solution

The following is a solution which demonstrates how to find the largest divisible subset in an array.

This solution uses Dynamic Programming to find the largest divisible subset.





		
		
			2. Largest Divisible Subset - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 14, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the largest divisible subset
// ============================================================================
public class Solution {
    public IList<int> LargestDivisibleSubset(int[] nums) {
        // Sort the array
        Array.Sort(nums);

        // List array of size n
        var dp = new List<int>[nums.Length];

        // Go through numbers
        var resultIndex = 0;
        for (int i = 0; i < nums.Length; ++i) {
            dp[i] = new List<int>();

            // Go through numbers that come before i and determine the maximum subset for i
            var currentMaxIndex = i;
            for (int j = 0; j < i; ++j) {
                // Check if the two numbers satisfies the condition
                if ((nums[i] % nums[j] == 0 || nums[j] % nums[i] == 0) && dp[currentMaxIndex].Count < dp[j].Count) {
                    currentMaxIndex = j;
                }
            }
            // Save items from max index to current dp index
            if (currentMaxIndex != i) {
                dp[i] = new List<int>(dp[currentMaxIndex]);
            }

            // Add current number to current dp index
            dp[i].Add(nums[i]);

            // Keep track of the largest subset
            if (dp[i].Count > dp[resultIndex].Count) {
                resultIndex = i;
            }
        }
        return dp[resultIndex];
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 14, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the largest divisible subset
// ============================================================================
public class Solution {
    public IList<int> LargestDivisibleSubset(int[] nums) {
        // Sort the array
        Array.Sort(nums);
 
        // List array of size n
        var dp = new List<int>[nums.Length];
 
        // Go through numbers
        var resultIndex = 0;
        for (int i = 0; i < nums.Length; ++i) {
            dp[i] = new List<int>();
 
            // Go through numbers that come before i and determine the maximum subset for i
            var currentMaxIndex = i;
            for (int j = 0; j < i; ++j) {
                // Check if the two numbers satisfies the condition
                if ((nums[i] % nums[j] == 0 || nums[j] % nums[i] == 0) && dp[currentMaxIndex].Count < dp[j].Count) {
                    currentMaxIndex = j;
                }
            }
            // Save items from max index to current dp index
            if (currentMaxIndex != i) {
                dp[i] = new List<int>(dp[currentMaxIndex]);
            }
 
            // Add current number to current dp index
            dp[i].Add(nums[i]);
 
            // Keep track of the largest subset
            if (dp[i].Count > dp[resultIndex].Count) {
                resultIndex = i;
            }
        }
        return dp[resultIndex];
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[1,2] [1,2,4,8]

C# || Online Stock Span – How To Get Daily Price Stock Quotes & Consecutive Day Span Using C#

November 12, 2021 admin No comments

The following is a module with functions which demonstrates how to get the daily price stock quotes & consecutive day span using C#.

1. Stock Spanner – Problem Statement

Design an algorithm that collects daily price quotes for some stock and returns the span of that stock’s price for the current day.

The span of the stock’s price today is defined as the maximum number of consecutive days (starting from today and going backward) for which the stock price was less than or equal to today’s price.

For example, if the price of a stock over the next 7 days were [100,80,60,70,60,75,85], then the stock spans would be [1,1,1,2,1,4,6].

Implement the StockSpanner class:

StockSpanner() Initializes the object of the class.
int next(int price) Returns the span of the stock’s price given that today’s price is price.

Example 1:

Input: ["StockSpanner", "next", "next", "next", "next", "next", "next", "next"] [[], [100], [80], [60], [70], [60], [75], [85]] Output: [null, 1, 1, 1, 2, 1, 4, 6]
Explanation: StockSpanner stockSpanner = new StockSpanner(); stockSpanner.next(100); // return 1 stockSpanner.next(80); // return 1 stockSpanner.next(60); // return 1 stockSpanner.next(70); // return 2 stockSpanner.next(60); // return 1 stockSpanner.next(75); // return 4, because the last 4 prices (including today's price of 75) were less than or equal to today's price. stockSpanner.next(85); // return 6

2. Stock Spanner – Solution

The following is a solution which demonstrates how to get the daily price stock quotes & consecutive day span.

This solution uses the monotonic stack approach.

The idea of this solution is to have a stack of a pair to store the current price and the maximum number of consecutive days.

For each new price, we check the top of the stack and keep a running total of each previous consecutive day span found for all stock prices that are less than or equal to today’s price.

Then, we add today’s price and the current running consecutive day total to the stack.





		
		
			2. Stock Spanner - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 12, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the daily price stock quotes day span
// ============================================================================
public class StockSpanner {
    // Store the current price & maximum number of consecutive days
    Stack<KeyValuePair<int, int>> stack;

    public StockSpanner() {
        stack = new Stack<KeyValuePair<int, int>>();
    }

    public int Next(int price) {
        var consecutiveDays = 1;

        // Compare current price with the item on the top of the stack
        while (stack.Count > 0 && stack.Peek().Key <= price) {
            // Get the previous consecutive day span and add to the current result
            consecutiveDays += stack.Peek().Value;
            stack.Pop();
        }
        // Add the current price and consecutive day span to the stack
        stack.Push(new KeyValuePair<int, int>(price, consecutiveDays));

        return consecutiveDays;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 12, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the daily price stock quotes day span
// ============================================================================
public class StockSpanner {
    // Store the current price & maximum number of consecutive days
    Stack<KeyValuePair<int, int>> stack;
 
    public StockSpanner() {
        stack = new Stack<KeyValuePair<int, int>>();
    }
 
    public int Next(int price) {
        var consecutiveDays = 1;
 
        // Compare current price with the item on the top of the stack
        while (stack.Count > 0 && stack.Peek().Key <= price) {
            // Get the previous consecutive day span and add to the current result
            consecutiveDays += stack.Peek().Value;
            stack.Pop();
        }
        // Add the current price and consecutive day span to the stack
        stack.Push(new KeyValuePair<int, int>(price, consecutiveDays));
 
        return consecutiveDays;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[null,1,1,1,2,1,4,6]

C# || How To Find Number Of Valid Words For Each Puzzle Using C#

November 09, 2021 admin No comments

The following is a module with functions which demonstrates how to find the number of valid words for each puzzle using C#.

1. Find Num Of Valid Words – Problem Statement

With respect to a given puzzle string, a word is valid if both the following conditions are satisfied:

word contains the first letter of puzzle.
For each letter in word, that letter is in puzzle.
- For example, if the puzzle is “abcdefg”, then valid words are “faced”, “cabbage”, and “baggage”, while
- invalid words are “beefed” (does not include ‘a’) and “based” (includes ‘s’ which is not in the puzzle).

Return an array answer, where answer[i] is the number of words in the given word list words that is valid with respect to the puzzle puzzles[i].

Example 1:

Input: words = ["aaaa","asas","able","ability","actt","actor","access"], puzzles = ["aboveyz","abrodyz","abslute","absoryz","actresz","gaswxyz"] Output: [1,1,3,2,4,0] Explanation: 1 valid word for "aboveyz" : "aaaa" 1 valid word for "abrodyz" : "aaaa" 3 valid words for "abslute" : "aaaa", "asas", "able" 2 valid words for "absoryz" : "aaaa", "asas" 4 valid words for "actresz" : "aaaa", "asas", "actt", "access" There are no valid words for "gaswxyz" cause none of the words in the list contains letter 'g'.

Example 2:

Input: words = ["apple","pleas","please"], puzzles = ["aelwxyz","aelpxyz","aelpsxy","saelpxy","xaelpsy"] Output: [0,1,3,2,0]

2. Find Num Of Valid Words – Solution

The following is a solution which demonstrates how to find the number of valid words for each puzzle.

This solution uses a Trie to find the number of valid words.





		
		
			2. Find Num Of Valid Words - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 9, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find number of valid words in a puzzle
// ============================================================================
public class Solution {
    public IList<int> FindNumOfValidWords(string[] words, string[] puzzles) {
        // Add words to the Trie
        var trie = new Trie();
        foreach (var word in words) {
            // Get distinct characters in the word and sort it
            var chars = word.Distinct().ToArray();

            // Longer words are never valid
            if (chars.Length <= 7) {
                Array.Sort(chars);
                trie.Insert(new string(chars));
            }
        }

        // Check how many words in the puzzle match in the Trie
        var result = new List<int>();
        foreach (var word in puzzles) {
            result.Add(trie.Search(word));
        }
        return result;
    }

    // Trie
    public class Trie {
        private TrieNode root;

        public Trie() {
            root = new TrieNode();
        }
        public void Insert(string word) {
            var node = root;
            foreach (var ch in word) {
                if (!node.ContainsKey(ch)) {
                    node.Add(ch, new TrieNode());
                }
                node = node.Get(ch);
            }
            node.SetComplete();
        }
        public int Search(string word) {
            return DFS(root, word, false);
        }
        private int DFS(TrieNode node, string word, bool firstFound) {
            var result = firstFound ? node.WordCount() : 0;
            foreach (var ch in word) {
                if (node.ContainsKey(ch)) {
                    result += DFS(node.Get(ch), word, firstFound || ch == word[0]);
                }
            }
            return result;
        }
    }

    // TrieNode
    public class TrieNode {
        private Dictionary<char, TrieNode> children;
        private bool isComplete;
        private int count;

        public TrieNode() {
            children = new Dictionary<char, TrieNode>();
        }
        public bool ContainsKey(char ch) {
            return children.ContainsKey(ch);
        }
        public TrieNode Get(char ch) {
            return children[ch];
        }
        public void Add(char ch, TrieNode node) {
            children[ch] = node;
        }
        public void SetComplete() {
            isComplete = true;
            ++count;
        }
        public bool IsComplete() {
            return isComplete;
        }
        public int WordCount() {
            return count;
        }
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 9, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find number of valid words in a puzzle
// ============================================================================
public class Solution {
    public IList<int> FindNumOfValidWords(string[] words, string[] puzzles) {
        // Add words to the Trie
        var trie = new Trie();
        foreach (var word in words) {
            // Get distinct characters in the word and sort it
            var chars = word.Distinct().ToArray();
 
            // Longer words are never valid
            if (chars.Length <= 7) {
                Array.Sort(chars);
                trie.Insert(new string(chars));
            }
        }
 
        // Check how many words in the puzzle match in the Trie
        var result = new List<int>();
        foreach (var word in puzzles) {
            result.Add(trie.Search(word));
        }
        return result;
    }
 
    // Trie
    public class Trie {
        private TrieNode root;
 
        public Trie() {
            root = new TrieNode();
        }
        public void Insert(string word) {
            var node = root;
            foreach (var ch in word) {
                if (!node.ContainsKey(ch)) {
                    node.Add(ch, new TrieNode());
                }
                node = node.Get(ch);
            }
            node.SetComplete();
        }
        public int Search(string word) {
            return DFS(root, word, false);
        }
        private int DFS(TrieNode node, string word, bool firstFound) {
            var result = firstFound ? node.WordCount() : 0;
            foreach (var ch in word) {
                if (node.ContainsKey(ch)) {
                    result += DFS(node.Get(ch), word, firstFound || ch == word[0]);
                }
            }
            return result;
        }
    }
 
    // TrieNode
    public class TrieNode {
        private Dictionary<char, TrieNode> children;
        private bool isComplete;
        private int count;
 
        public TrieNode() {
            children = new Dictionary<char, TrieNode>();
        }
        public bool ContainsKey(char ch) {
            return children.ContainsKey(ch);
        }
        public TrieNode Get(char ch) {
            return children[ch];
        }
        public void Add(char ch, TrieNode node) {
            children[ch] = node;
        }
        public void SetComplete() {
            isComplete = true;
            ++count;
        }
        public bool IsComplete() {
            return isComplete;
        }
        public int WordCount() {
            return count;
        }
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[1,1,3,2,4,0] [0,1,3,2,0]

C# || How To Implement Trie Prefix Tree Using C#

November 09, 2021 admin No comments

The following is a module with functions which demonstrates how to implement a trie prefix tree using C#.

1. Trie – Problem Statement

A trie (pronounced as “try”) or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.

Implement the Trie class:

Trie() Initializes the trie object.
void insert(String word) Inserts the string word into the trie.
boolean search(String word) Returns true if the string word is in the trie (i.e., was inserted before), and false otherwise.
boolean startsWith(String prefix) Returns true if there is a previously inserted string word that has the prefix prefix, and false otherwise.

Example 1:

Input ["Trie", "insert", "search", "search", "startsWith", "insert", "search"] [[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]] Output [null, null, true, false, true, null, true]
Explanation Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // return True trie.search("app"); // return False trie.startsWith("app"); // return True trie.insert("app"); trie.search("app"); // return True

2. Trie – Solution

The following is a solution which demonstrates how to implement a trie prefix tree.





		
		
			2. Trie - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 9, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to implement a trie prefix tree
// ============================================================================
// Trie
public class Trie {
    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }
    public void Insert(string word) {
        var node = root;
        foreach (var ch in word) {
            if (!node.ContainsKey(ch)) {
                node.Add(ch, new TrieNode());
            }
            node = node.Get(ch);
        }
        node.SetComplete();
    }
    // Search a prefix or whole key in trie and
    // returns the node where search ends
    public TrieNode SearchPrefix(string word) {
        var node = root;
        foreach (var ch in word) {
            if (node.ContainsKey(ch)) {
                node = node.Get(ch);
            } else {
                return null;
            }
        }
        return node;
    }
    public bool Search(string word) {
        var node = SearchPrefix(word);
        return node != null && node.IsComplete();
    }
    public bool StartsWith(string prefix) {
        var node = SearchPrefix(prefix);
        return node != null;
    }
}

// TrieNode
public class TrieNode {
    private Dictionary<char, TrieNode> children;
    private bool isComplete;
    private int count;

    public TrieNode() {
        children = new Dictionary<char, TrieNode>();
    }
    public bool ContainsKey(char ch) {
        return children.ContainsKey(ch);
    }
    public TrieNode Get(char ch) {
        return children[ch];
    }
    public void Add(char ch, TrieNode node) {
        children[ch] = node;
    }
    public void SetComplete() {
        isComplete = true;
        ++count;
    }
    public bool IsComplete() {
        return isComplete;
    }
    public int WordCount() {
        return count;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 9, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to implement a trie prefix tree
// ============================================================================
// Trie
public class Trie {
    private TrieNode root;
 
    public Trie() {
        root = new TrieNode();
    }
    public void Insert(string word) {
        var node = root;
        foreach (var ch in word) {
            if (!node.ContainsKey(ch)) {
                node.Add(ch, new TrieNode());
            }
            node = node.Get(ch);
        }
        node.SetComplete();
    }
    // Search a prefix or whole key in trie and
    // returns the node where search ends
    public TrieNode SearchPrefix(string word) {
        var node = root;
        foreach (var ch in word) {
            if (node.ContainsKey(ch)) {
                node = node.Get(ch);
            } else {
                return null;
            }
        }
        return node;
    }
    public bool Search(string word) {
        var node = SearchPrefix(word);
        return node != null && node.IsComplete();
    }
    public bool StartsWith(string prefix) {
        var node = SearchPrefix(prefix);
        return node != null;
    }
}
 
// TrieNode
public class TrieNode {
    private Dictionary<char, TrieNode> children;
    private bool isComplete;
    private int count;
 
    public TrieNode() {
        children = new Dictionary<char, TrieNode>();
    }
    public bool ContainsKey(char ch) {
        return children.ContainsKey(ch);
    }
    public TrieNode Get(char ch) {
        return children[ch];
    }
    public void Add(char ch, TrieNode node) {
        children[ch] = node;
    }
    public void SetComplete() {
        isComplete = true;
        ++count;
    }
    public bool IsComplete() {
        return isComplete;
    }
    public int WordCount() {
        return count;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[null,null,true,false,true,null,true]

C# || How To Find Friends Of Appropriate Ages Using C#

November 05, 2021 admin No comments

The following is a module with functions which demonstrates how to find friends of appropriate ages using C#.

1. Num Friend Requests – Problem Statement

There are n persons on a social media website. You are given an integer array ages where ages[i] is the age of the i^th person.

A Person x will not send a friend request to a person y (x != y) if any of the following conditions is true:

age[y] <= 0.5 * age[x] + 7
age[y] > age[x]
age[y] > 100 && age[x] < 100

Otherwise, x will send a friend request to y.

Note that if x sends a request to y, y will not necessarily send a request to x. Also, a person will not send a friend request to themself.

Return the total number of friend requests made.

Example 1:

Input: ages = [16,16] Output: 2 Explanation: 2 people friend request each other.

Example 2:

Input: ages = [16,17,18] Output: 2 Explanation: Friend requests are made 17 -> 16, 18 -> 17.

Example 3:

Input: ages = [20,30,100,110,120] Output: 3 Explanation: Friend requests are made 110 -> 100, 120 -> 110, 120 -> 100.

2. Num Friend Requests – Solution

The following is a solution which demonstrates how to find friends of appropriate ages.

In this solution, we sort the ages and use a map that keeps track of the ages, and the total friend request count that age can recieve.

Binary search is used to get the age range in the array that satisfies the friend request conditions for a given age.





		
		
			2. Num Friend Requests - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 5, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find friends of appropriate ages
// ============================================================================
public class Solution {
    public int NumFriendRequests(int[] ages) {
        var result = 0;

        // Sort ages
        Array.Sort(ages);

        // Keep track of results calculated
        var seen = new Dictionary<int, int>();

        // Iterate array backwards
        for (int index = ages.Length - 1; index >= 0; --index) {
            // Check if we already calculated result for age
            if (!seen.ContainsKey(ages[index])) {
                // Binary search
                var lo = 0;
                var hi = index;
                while (lo < hi) {
                    var mid = lo + (hi - lo) / 2;

                    // Check if friends can be made in this range
                    if (!CanFriend(ages[index], ages[mid])) {
                        lo = mid + 1;
                    } else {
                        hi = mid;
                    }
                }
                // Get distance between index and hi. This is the friend count for the age
                seen[ages[index]] = index - hi;
            }
            // Update result count
            result += seen[ages[index]];
        }

        return result;
    }

    private bool CanFriend(int x, int y) {
        return !((y > x) || (y > 100 && x < 100) || (y <= 0.5 * x + 7));
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 5, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find friends of appropriate ages
// ============================================================================
public class Solution {
    public int NumFriendRequests(int[] ages) {
        var result = 0;
 
        // Sort ages
        Array.Sort(ages);
 
        // Keep track of results calculated
        var seen = new Dictionary<int, int>();
 
        // Iterate array backwards
        for (int index = ages.Length - 1; index >= 0; --index) {
            // Check if we already calculated result for age
            if (!seen.ContainsKey(ages[index])) {
                // Binary search
                var lo = 0;
                var hi = index;
                while (lo < hi) {
                    var mid = lo + (hi - lo) / 2;
 
                    // Check if friends can be made in this range
                    if (!CanFriend(ages[index], ages[mid])) {
                        lo = mid + 1;
                    } else {
                        hi = mid;
                    }
                }
                // Get distance between index and hi. This is the friend count for the age
                seen[ages[index]] = index - hi;
            }
            // Update result count
            result += seen[ages[index]];
        }
 
        return result;
    }
 
    private bool CanFriend(int x, int y) {
        return !((y > x) || (y > 100 && x < 100) || (y <= 0.5 * x + 7));
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

2 2 3

C# || How To Get Total Sum Of Left Leaves In Binary Tree Using C#

November 03, 2021 admin No comments

The following is a module with functions which demonstrates how to get the total sum of left leaves in a binary tree using C#.

1. Sum Of Left Leaves – Problem Statement

Given the root of a binary tree, return the sum of all left leaves.

A leaf node is a node with no children.

Example 1:

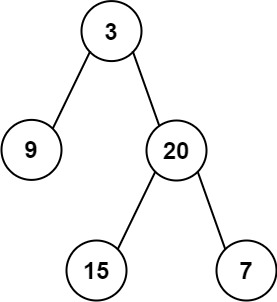
Input: root = [3,9,20,null,null,15,7] Output: 24 Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.

Example 2:

Input: root = [1] Output: 0

2. Sum Of Left Leaves – Solution

The following are two solutions which demonstrates how to get the total sum of left leaves in a binary tree.

Both solutions use Depth First Search to explore items at each level.

In both solutions, we traverse the left and right side of the tree, keeping track of which node is the ‘left’ node.

When a leaf is encountered and its a node on the left side, we increment the final result with the value of the node on the left side.

Recursive





		
		
			2. Sum Of Left Leaves - Recursive - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the sum of left leaves
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumOfLeftLeaves(TreeNode root) {
        return Traverse(root, false);
    }

    private int Traverse(TreeNode node, bool isLeft) {
        if (node == null) {
            return 0;
        }
        // We have reached a leaf node
        if (node.left == null && node.right == null) {
            return isLeft ? node.val : 0;
        }
        // Keep traversing left and right looking for left leaves
        return Traverse(node.left, true) + Traverse(node.right, false);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the sum of left leaves
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumOfLeftLeaves(TreeNode root) {
        return Traverse(root, false);
    }
 
    private int Traverse(TreeNode node, bool isLeft) {
        if (node == null) {
            return 0;
        }
        // We have reached a leaf node
        if (node.left == null && node.right == null) {
            return isLeft ? node.val : 0;
        }
        // Keep traversing left and right looking for left leaves
        return Traverse(node.left, true) + Traverse(node.right, false);
    }
}// http://programmingnotes.org/

Iterative





		
		
			2. Sum Of Left Leaves - Iterative - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the sum of left leaves
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // Declare stack
        var stack = new Stack<KeyValuePair<TreeNode, bool>>();
        var result = 0;

        // Add root to stack
        stack.Push(new KeyValuePair<TreeNode, bool>(root, false));

        // Loop through items on the stack
        while (stack.Count > 0) {
            // Get current node and value indicating if its a left node
            var current = stack.Pop();
            var node = current.Key;
            var isLeft = current.Value;

            // We have reached a leaf node
            if (node.left == null && node.right == null) {
                result += isLeft ? node.val : 0;
            } else {
                // Keep traversing left and right looking for left leaves
                if (node.left != null) {
                    stack.Push(new KeyValuePair<TreeNode, bool>(node.left, true));
                }
                if (node.right != null) {
                    stack.Push(new KeyValuePair<TreeNode, bool>(node.right, false));
                }
            }
        }

        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get the sum of left leaves
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // Declare stack
        var stack = new Stack<KeyValuePair<TreeNode, bool>>();
        var result = 0;
 
        // Add root to stack
        stack.Push(new KeyValuePair<TreeNode, bool>(root, false));
 
        // Loop through items on the stack
        while (stack.Count > 0) {
            // Get current node and value indicating if its a left node
            var current = stack.Pop();
            var node = current.Key;
            var isLeft = current.Value;
 
            // We have reached a leaf node
            if (node.left == null && node.right == null) {
                result += isLeft ? node.val : 0;
            } else {
                // Keep traversing left and right looking for left leaves
                if (node.left != null) {
                    stack.Push(new KeyValuePair<TreeNode, bool>(node.left, true));
                }
                if (node.right != null) {
                    stack.Push(new KeyValuePair<TreeNode, bool>(node.right, false));
                }
            }
        }
 
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

24 0

C# || How To Get Total Sum Root To Leaf Numbers In Binary Tree Using C#

November 03, 2021 admin No comments

The following is a module with functions which demonstrates how to get the total sum root to leaf numbers in a binary tree using C#.

1. Sum Numbers – Problem Statement

You are given the root of a binary tree containing digits from 0 to 9 only.

Each root-to-leaf path in the tree represents a number.

For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.

Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.

A leaf node is a node with no children.

Example 1:

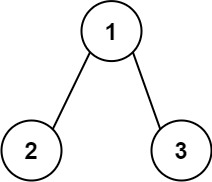
Input: root = [1,2,3] Output: 25 Explanation: The root-to-leaf path 1->2 represents the number 12. The root-to-leaf path 1->3 represents the number 13. Therefore, sum = 12 + 13 = 25.

Example 2:

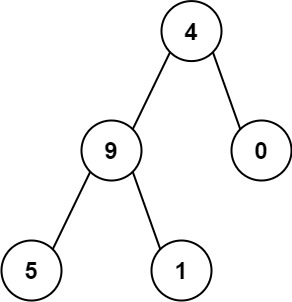
Input: root = [4,9,0,5,1] Output: 1026 Explanation: The root-to-leaf path 4->9->5 represents the number 495. The root-to-leaf path 4->9->1 represents the number 491. The root-to-leaf path 4->0 represents the number 40. Therefore, sum = 495 + 491 + 40 = 1026.

2. Sum Numbers – Solution

The following are two solutions which demonstrates how to get the total sum root to leaf numbers in a binary tree.

Both solutions use Depth First Search to explore items at each level.

Recursive





		
		
			2. Sum Numbers - Recursive - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get sum root to leaf numbers
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumNumbers(TreeNode root) {
        return Traverse(root, 0);
    }

    private int Traverse(TreeNode node, int currentSum) {
        if (node == null) {
            return 0;
        }

        // Calculate current sum
        currentSum = (currentSum * 10) + node.val;

        // We have reached a leaf node
        if (node.left == null && node.right == null) {
            return currentSum;
        }

        // Keep traversing left and right calculating the sum
        return Traverse(node.left, currentSum) + Traverse(node.right, currentSum);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get sum root to leaf numbers
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumNumbers(TreeNode root) {
        return Traverse(root, 0);
    }
 
    private int Traverse(TreeNode node, int currentSum) {
        if (node == null) {
            return 0;
        }
 
        // Calculate current sum
        currentSum = (currentSum * 10) + node.val;
 
        // We have reached a leaf node
        if (node.left == null && node.right == null) {
            return currentSum;
        }
 
        // Keep traversing left and right calculating the sum
        return Traverse(node.left, currentSum) + Traverse(node.right, currentSum);
    }
}// http://programmingnotes.org/

Iterative





		
		
			2. Sum Numbers - Iterative - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get sum root to leaf numbers
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumNumbers(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // Declare stack
        var stack = new Stack<KeyValuePair<TreeNode, int>>();
        var result = 0;

        // Add root to stack
        stack.Push(new KeyValuePair<TreeNode, int>(root, 0));

        // Loop through items on the stack
        while (stack.Count > 0) {
            // Get current node and running sum
            var current = stack.Pop();
            var node = current.Key;
            var currentSum = current.Value;

            // Calculate current sum
            currentSum = (currentSum * 10) + node.val;

            // We have reached a leaf node
            if (node.left == null && node.right == null) {
                result += currentSum;
            } else {
                // Keep traversing left and right calculating the sum
                if (node.left != null) {
                    stack.Push(new KeyValuePair<TreeNode, int>(node.left, currentSum));
                }
                if (node.right != null) {
                    stack.Push(new KeyValuePair<TreeNode, int>(node.right, currentSum));
                }
            }
        }
        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 3, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get sum root to leaf numbers
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public int SumNumbers(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // Declare stack
        var stack = new Stack<KeyValuePair<TreeNode, int>>();
        var result = 0;
 
        // Add root to stack
        stack.Push(new KeyValuePair<TreeNode, int>(root, 0));
 
        // Loop through items on the stack
        while (stack.Count > 0) {
            // Get current node and running sum
            var current = stack.Pop();
            var node = current.Key;
            var currentSum = current.Value;
 
            // Calculate current sum
            currentSum = (currentSum * 10) + node.val;
 
            // We have reached a leaf node
            if (node.left == null && node.right == null) {
                result += currentSum;
            } else {
                // Keep traversing left and right calculating the sum
                if (node.left != null) {
                    stack.Push(new KeyValuePair<TreeNode, int>(node.left, currentSum));
                }
                if (node.right != null) {
                    stack.Push(new KeyValuePair<TreeNode, int>(node.right, currentSum));
                }
            }
        }
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

25 1026

C# || Unique Paths III – How To Get The Number Of Paths From Start To End In Grid Matrix Using C#

November 02, 2021 admin No comments

The following is a module with functions which demonstrates how to get the number of paths from start to end in a grid matrix using C#.

1. Unique Paths III – Problem Statement

You are given an m x n integer array grid where grid[i][j] could be:

1 representing the starting square. There is exactly one starting square.
2 representing the ending square. There is exactly one ending square.
0 representing empty squares we can walk over.
-1 representing obstacles that we cannot walk over.

Return the number of 4-directional walks from the starting square to the ending square, that walk over every non-obstacle square exactly once.

Example 1:

Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,2,-1]] Output: 2 Explanation: We have the following two paths: 1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2) 2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

Example 2:

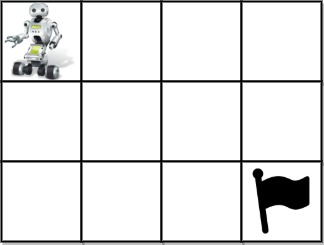
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,2]] Output: 4 Explanation: We have the following four paths: 1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3) 2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3) 3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3) 4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

Example 3:

Input: grid = [[0,1],[2,0]] Output: 0 Explanation: There is no path that walks over every empty square exactly once. Note that the starting and ending square can be anywhere in the grid.

2. Unique Paths III – Solution

The following is a solution which demonstrates how to get the number of paths from start to end in a grid matrix.

This solution uses Depth First Search when looking for paths.

In this solution, we find the starting coordinates and count the number of empty cells.

Then we do DFS, marking the visited positions and keeping track of the number of steps. If we reach the end and the number of steps matches the number of empty cells, we found a path.





		
		
			2. Unique Paths III - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 2, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get total paths in a grid matrix
// ============================================================================
public class Solution {
    private int START = 1;
    private int END = 2;
    private int EMPTY = 0;
    private int OBSTACLE = -1;

    public int UniquePathsIII(int[][] grid) {
        // Include the starting position in the empty cell count
        var emptyCellCount = 1;

        // The row/col coordinates of the starting point
        var startRow = -1;
        var startCol = -1;

        for (int row = 0; row < grid.Length; ++row) {
            for (int col = 0; col < grid[row].Length; ++col) {
                // Get empty cell count
                if (grid[row][col] == EMPTY) {
                    ++emptyCellCount;

                // Get the starting coordinates
                } else if (grid[row][col] == START) {
                    startRow = row;
                    startCol = col;
                }
            }
        }

        // Return total paths to the end
        return DFS(grid, startRow, startCol, emptyCellCount);
    }

    private int DFS(int[][] grid, int row, int col, int emptyCellCount) {
        // Make sure parameters are in bounds
        if (row < 0 || row >= grid.Length || col < 0 || col >= grid[row].Length) {
            return 0;
        }
        // Obstacle encountered or path already visited
        if (grid[row][col] == OBSTACLE) {
            return 0;
        }
        // We have reached the end
        if (grid[row][col] == END) {
            // Check to see if all empty cells have been used
            return emptyCellCount == 0 ? 1 : 0;
        }

        // Save the old value
        var oldValue = grid[row][col];

        // Mark path as visited
        grid[row][col] = OBSTACLE;

        // Get the path count in right, left, top, bottom direction
        var pathCount =
            // Search Right
            DFS(grid, row, col + 1, emptyCellCount - 1) +
            // Search Left
            DFS(grid, row, col - 1, emptyCellCount - 1) +
            // Search Top
            DFS(grid, row - 1, col, emptyCellCount - 1) +
            // Search Bottom
            DFS(grid, row + 1, col, emptyCellCount - 1);

        // Unmark path as visited
        grid[row][col] = oldValue;

        return pathCount;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 2, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to get total paths in a grid matrix
// ============================================================================
public class Solution {
    private int START = 1;
    private int END = 2;
    private int EMPTY = 0;
    private int OBSTACLE = -1;
 
    public int UniquePathsIII(int[][] grid) {
        // Include the starting position in the empty cell count
        var emptyCellCount = 1;
 
        // The row/col coordinates of the starting point
        var startRow = -1;
        var startCol = -1;
 
        for (int row = 0; row < grid.Length; ++row) {
            for (int col = 0; col < grid[row].Length; ++col) {
                // Get empty cell count
                if (grid[row][col] == EMPTY) {
                    ++emptyCellCount;
 
                // Get the starting coordinates
                } else if (grid[row][col] == START) {
                    startRow = row;
                    startCol = col;
                }
            }
        }
 
        // Return total paths to the end
        return DFS(grid, startRow, startCol, emptyCellCount);
    }
 
    private int DFS(int[][] grid, int row, int col, int emptyCellCount) {
        // Make sure parameters are in bounds
        if (row < 0 || row >= grid.Length || col < 0 || col >= grid[row].Length) {
            return 0;
        }
        // Obstacle encountered or path already visited
        if (grid[row][col] == OBSTACLE) {
            return 0;
        }
        // We have reached the end
        if (grid[row][col] == END) {
            // Check to see if all empty cells have been used
            return emptyCellCount == 0 ? 1 : 0;
        }
 
        // Save the old value
        var oldValue = grid[row][col];
 
        // Mark path as visited
        grid[row][col] = OBSTACLE;
 
        // Get the path count in right, left, top, bottom direction
        var pathCount =
            // Search Right
            DFS(grid, row, col + 1, emptyCellCount - 1) +
            // Search Left
            DFS(grid, row, col - 1, emptyCellCount - 1) +
            // Search Top
            DFS(grid, row - 1, col, emptyCellCount - 1) +
            // Search Bottom
            DFS(grid, row + 1, col, emptyCellCount - 1);
 
        // Unmark path as visited
        grid[row][col] = oldValue;
 
        return pathCount;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

2 4 0

C# || How To Capture All Surrounded Regions ‘X’ & ‘O’ In Board Matrix Using C#

November 01, 2021 admin No comments

The following is a module with functions which demonstrates how to capture all surrounded regions ‘X’ and ‘O’ in a board matrix using C#.

1. Surrounded Regions – Problem Statement

Given an m x n matrix board containing ‘X’ and ‘O’, capture all regions that are 4-directionally surrounded by ‘X’.

A region is captured by flipping all ‘O’s into ‘X’s in that surrounded region.

Example 1:

Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]] Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]] Explanation: Surrounded regions should not be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

Example 2:

Input: board = [["X"]] Output: [["X"]]

2. Surrounded Regions – Solution

The following is a solution which demonstrates how to capture all surrounded regions ‘X’ and ‘O’ in a board matrix.

This solution uses Breadth First Search when looking for surrounded regions.

A ‘O’ is surrounded if there is no path from it to the outer border of the matrix (i.e: row: index 0, column: index 0, row: index matrix.length-1, column: index matrix[0].length-1) when moving in a North, South, East, or West direction.

Basically:

A 'O' will not be flipped to 'X' if: It is on the border, OR It is connected to any other 'O' that cannot be flipped

In this solution we get all ‘O’ cells around the borders and keep track of all ‘O’ cells connected to the ones around the outer border.

We mark the border ‘O’ cells, and all the connected ‘O’ cells to the ones around the outer border as invalid.

In the end, we mark all valid ‘O’ cells as ‘X’.





		
		
			2. Surrounded Regions - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 1, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to flip surrounded regions
// ============================================================================
public class Solution {
    public void Solve(char[][] board) {
        var queue = new Queue<KeyValuePair<int, int>>();

        // Get coordinates of 'O' cells on the left and right border and add to queue
        for (int row = 0; row < board.Length; ++row) {
            // Check left border
            if (board[row][0] == 'O') {
                queue.Enqueue(new KeyValuePair<int, int>(row, 0));
            }
            // Check right border
            if(board[row][board[row].Length - 1] == 'O') {
                queue.Enqueue(new KeyValuePair<int, int>(row, board[row].Length - 1));
            }
        }

        // Get coordinates of 'O' cells on the top and bottom border and add to queue
        for (int col = 0; col < board[0].Length; ++col) {
            // Check top border
            if (board[0][col] == 'O') {
                queue.Enqueue(new KeyValuePair<int, int>(0, col));
            }
            // Check bottom border
            if (board[board.Length - 1][col] == 'O') {
                queue.Enqueue(new KeyValuePair<int, int>(board.Length - 1, col));
            }
        }

        // 2D bool array to keep track of 'O' cells connected to the ones on the outer border
        var visited = new bool[board.Length][];
        for (int row = 0; row < board.Length; ++row) {
            visited[row] = new bool[board[row].Length];
        }

        // Search directions
        var directions = new List<KeyValuePair<int, int>>() {
            // Right
            new KeyValuePair<int, int>(0, 1),
            // Left
            new KeyValuePair<int, int>(0, -1),
            // Top
            new KeyValuePair<int, int>(-1, 0),
            // Bottom
            new KeyValuePair<int, int>(1, 0),
        };

        // Find all 'O' cells connected to the ones on the outer border
        while (queue.Count > 0) {
            var current = queue.Dequeue();

            // Get current coordinates
            var currentRow = current.Key;
            var currentCol = current.Value;

            // Mark cell as visited, which means its connected to a border cell
            visited[currentRow][currentCol] = true;

            // Search right, left, top, bottom for connected 'O' cells
            foreach (var direction in directions) {
                var newRow = currentRow + direction.Key;
                var newCol = currentCol + direction.Value;

                // Add connected cells to the queue
                if (IsValidCell(board, newRow, newCol) && board[newRow][newCol] == 'O' && !visited[newRow][newCol]) {
                    queue.Enqueue(new KeyValuePair<int, int>(newRow, newCol));
                }
            }
        }

        // Mark the 'O' cells not connected to outer borders as X
        for (int row = 0; row < board.Length; ++row) {
            for (int col = 0; col < board[row].Length; ++col) {
                if (board[row][col] == 'O' && !visited[row][col]) {
                    board[row][col] = 'X';
                }
            }
        }
    }

    private bool IsValidCell(char[][] board, int row, int col) {
        return row >= 0 && row < board.Length && col >= 0 && col < board[row].Length;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Nov 1, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to flip surrounded regions
// ============================================================================
public class Solution {
    public void Solve(char[][] board) {
        var queue = new Queue<KeyValuePair<int, int>>();
 
        // Get coordinates of 'O' cells on the left and right border and add to queue
        for (int row = 0; row < board.Length; ++row) {
            // Check left border
            if (board[row][0] == 'O') {
                queue.Enqueue(new KeyValuePair<int, int>(row, 0));
            }
            // Check right border
            if(board[row][board[row].Length - 1] == 'O') {
                queue.Enqueue(new KeyValuePair<int, int>(row, board[row].Length - 1));
            }
        }
 
        // Get coordinates of 'O' cells on the top and bottom border and add to queue
        for (int col = 0; col < board[0].Length; ++col) {
            // Check top border
            if (board[0][col] == 'O') {
                queue.Enqueue(new KeyValuePair<int, int>(0, col));
            }
            // Check bottom border
            if (board[board.Length - 1][col] == 'O') {
                queue.Enqueue(new KeyValuePair<int, int>(board.Length - 1, col));
            }
        }
 
        // 2D bool array to keep track of 'O' cells connected to the ones on the outer border
        var visited = new bool[board.Length][];
        for (int row = 0; row < board.Length; ++row) {
            visited[row] = new bool[board[row].Length];
        }
 
        // Search directions
        var directions = new List<KeyValuePair<int, int>>() {
            // Right
            new KeyValuePair<int, int>(0, 1),
            // Left
            new KeyValuePair<int, int>(0, -1),
            // Top
            new KeyValuePair<int, int>(-1, 0),
            // Bottom
            new KeyValuePair<int, int>(1, 0),
        };
 
        // Find all 'O' cells connected to the ones on the outer border
        while (queue.Count > 0) {
            var current = queue.Dequeue();
 
            // Get current coordinates
            var currentRow = current.Key;
            var currentCol = current.Value;
 
            // Mark cell as visited, which means its connected to a border cell
            visited[currentRow][currentCol] = true;
 
            // Search right, left, top, bottom for connected 'O' cells
            foreach (var direction in directions) {
                var newRow = currentRow + direction.Key;
                var newCol = currentCol + direction.Value;
 
                // Add connected cells to the queue
                if (IsValidCell(board, newRow, newCol) && board[newRow][newCol] == 'O' && !visited[newRow][newCol]) {
                    queue.Enqueue(new KeyValuePair<int, int>(newRow, newCol));
                }
            }
        }
 
        // Mark the 'O' cells not connected to outer borders as X
        for (int row = 0; row < board.Length; ++row) {
            for (int col = 0; col < board[row].Length; ++col) {
                if (board[row][col] == 'O' && !visited[row][col]) {
                    board[row][col] = 'X';
                }
            }
        }
    }
 
    private bool IsValidCell(char[][] board, int row, int col) {
        return row >= 0 && row < board.Length && col >= 0 && col < board[row].Length;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]] [["X"]]

C# || How To Flatten A Multilevel Doubly Linked List Using C#

October 30, 2021 admin No comments

The following is a module with functions which demonstrates how to flatten a doubly linked list using C#.

1. Flatten – Problem Statement

You are given a doubly linked list which in addition to the next and previous pointers, it could have a child pointer, which may or may not point to a separate doubly linked list. These child lists may have one or more children of their own, and so on, to produce a multilevel data structure, as shown in the example below.

Flatten the list so that all the nodes appear in a single-level, doubly linked list. You are given the head of the first level of the list.

Example 1:

Input: head = [1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12] Output: [1,2,3,7,8,11,12,9,10,4,5,6] Explanation:
The multilevel linked list in the input is as follows:

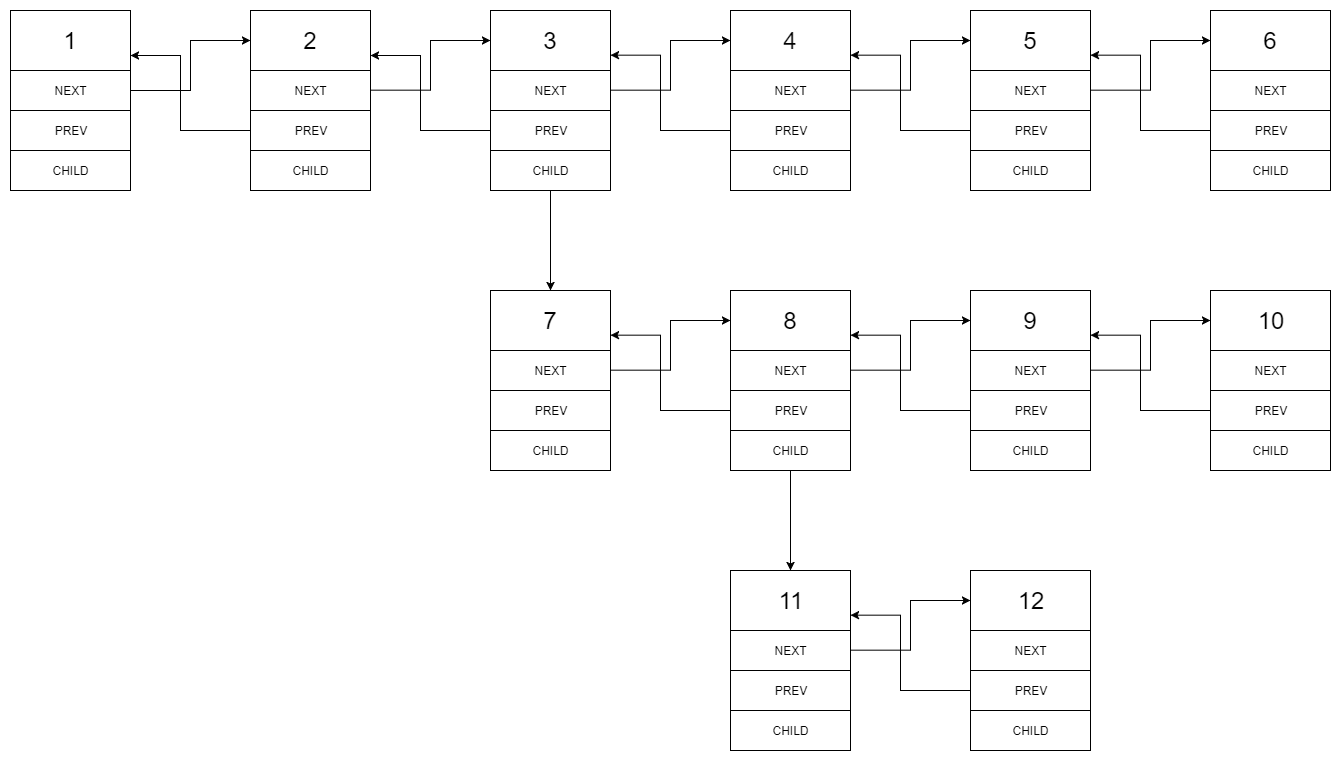
After flattening the multilevel linked list it becomes:

Example 2:

Input: head = [1,2,null,3] Output: [1,3,2] Explanation:
The input multilevel linked list is as follows:
1---2---NULL | 3---NULL

Example 3:

Input: head = [] Output: []

2. Flatten – Solution

The following are two solutions which demonstrates how to flatten a doubly linked list.

Iterative





		
		
			2. Flatten Iterative - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to flatten a doubly linked list
// ============================================================================
/*
// Definition for a Node.
public class Node {
    public int val;
    public Node prev;
    public Node next;
    public Node child;
}
*/
public class Solution {
    public Node Flatten(Node head) {
        var current = head;
        var stack = new Stack<Node>();

        // Loop through nodes
        while (current != null) {

            // Check to see if node has child
            if (current.child != null) {
                // If current node has a next node, save to stack
                // so we can reconnect it to the tail
                // of the child node later
                if (current.next != null) {
                    stack.Push(current.next);
                }

                // Set the next node as the child,
                // we will now iterate down this path
                current.next = current.child;

                // Set the previous node as the current
                current.next.prev = current;

                // Set child to null
                current.child = null;

            } else if (current.next == null) {
                // Reconnect node at the top of the
                // stack to the tail child node
                if (stack.Count > 0) {
                    // Set the next node as the reconnected node,
                    // we will now iterate down this path
                    current.next = stack.Pop();
                    current.next.prev = current;
                }
            }
            current = current.next;
        }

        return head;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to flatten a doubly linked list
// ============================================================================
/*
// Definition for a Node.
public class Node {
    public int val;
    public Node prev;
    public Node next;
    public Node child;
}
*/
public class Solution {
    public Node Flatten(Node head) {
        var current = head;
        var stack = new Stack<Node>();
 
        // Loop through nodes
        while (current != null) {
 
            // Check to see if node has child
            if (current.child != null) {
                // If current node has a next node, save to stack
                // so we can reconnect it to the tail
                // of the child node later
                if (current.next != null) {
                    stack.Push(current.next);
                }
 
                // Set the next node as the child,
                // we will now iterate down this path
                current.next = current.child;
 
                // Set the previous node as the current
                current.next.prev = current;
 
                // Set child to null
                current.child = null;
 
            } else if (current.next == null) {
                // Reconnect node at the top of the
                // stack to the tail child node
                if (stack.Count > 0) {
                    // Set the next node as the reconnected node,
                    // we will now iterate down this path
                    current.next = stack.Pop();
                    current.next.prev = current;
                }
            }
            current = current.next;
        }
 
        return head;
    }
}// http://programmingnotes.org/

Recursive





		
		
			2. Flatten Recursive - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to flatten a doubly linked list
// ============================================================================
/*
// Definition for a Node.
public class Node {
    public int val;
    public Node prev;
    public Node next;
    public Node child;
}
*/
public class Solution {
    public Node Flatten(Node head) {
        Flatten(head, null);
        return head;
    }

    private Node Flatten(Node current, Node previous) {
        if (current == null) {
            return previous;
        }

        // If previous node exists, set the next and previous values
        if (previous != null) {
            previous.next = current;
            current.prev = previous;
        }

        // Save the next node so we can reconnect it to the tail
        // of the child node later
        var next = current.next;

        // Traverse down child path.
        // If children exist, this returns the last child for the current node
        var tail = Flatten(current.child, current);

        // Child path has been explored, set to null
        current.child = null;

        // Reconnect the next node to the tail child node
        return Flatten(next, tail);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to flatten a doubly linked list
// ============================================================================
/*
// Definition for a Node.
public class Node {
    public int val;
    public Node prev;
    public Node next;
    public Node child;
}
*/
public class Solution {
    public Node Flatten(Node head) {
        Flatten(head, null);
        return head;
    }
 
    private Node Flatten(Node current, Node previous) {
        if (current == null) {
            return previous;
        }
 
        // If previous node exists, set the next and previous values
        if (previous != null) {
            previous.next = current;
            current.prev = previous;
        }
 
        // Save the next node so we can reconnect it to the tail
        // of the child node later
        var next = current.next;
 
        // Traverse down child path.
        // If children exist, this returns the last child for the current node
        var tail = Flatten(current.child, current);
 
        // Child path has been explored, set to null
        current.child = null;
 
        // Reconnect the next node to the tail child node
        return Flatten(next, tail);
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[1,2,3,7,8,11,12,9,10,4,5,6] [1,3,2] []

C# || How To Traverse Binary Tree Zigzag Level Order Using C#

October 30, 2021 admin No comments

The following is a module with functions which demonstrates how to traverse binary tree zigzag level order using C#.

1. Zigzag Level Order – Problem Statement

Given the root of a binary tree, return the zigzag level order traversal of its nodes’ values. (i.e., from left to right, then right to left for the next level and alternate between).

Example 1:

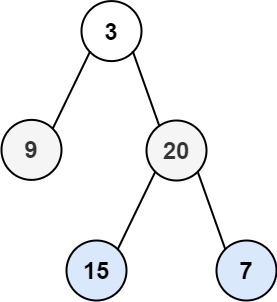
Input: root = [3,9,20,null,null,15,7] Output: [[3],[20,9],[15,7]]

Example 2:

Input: root = [1] Output: [[1]]

Example 3:

Input: root = [] Output: []

2. Zigzag Level Order – Solution

The following is a solution which demonstrates how to traverse binary tree zigzag level order.

This solution uses Breadth First Search to explore items at each level.





		
		
			2. Zigzag Level Order - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 29, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to traverse a tree zigzag level order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public IList<IList<int>> ZigzagLevelOrder(TreeNode root) {
        var result = new List<IList<int>>();
        var stack = new Stack<TreeNode>();

        // Add root to stack
        if (root != null) {
            stack.Push(root);
        }

        var leftToRight = true;
        while (stack.Count > 0) {
            var queue = new Queue<TreeNode>();
            var level = new List<int>();

            // Add items at the top of the stack to the current level
            for (var itemCount = stack.Count; itemCount > 0; --itemCount) {
                var current = stack.Peek();
                stack.Pop();

                level.Add(current.val);
                queue.Enqueue(current);
            }

            // Add level to result
            result.Add(level);

            // Go through items in the queue and add them to the stack in the proper order
            for (var itemCount = queue.Count; itemCount > 0; --itemCount) {
                var current = queue.Peek();
                queue.Dequeue();

                // Add children to the stack
                // Left to right or Right to left order
                if (leftToRight) {
                    if (current.left != null) {
                        stack.Push(current.left);
                    }
                    if (current.right != null) {
                        stack.Push(current.right);
                    }
                } else {
                    if (current.right != null) {
                        stack.Push(current.right);
                    }
                    if (current.left != null) {
                        stack.Push(current.left);
                    }
                }
            }
            // Alternate order for the next level
            leftToRight = !leftToRight;
        }
        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 29, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to traverse a tree zigzag level order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public IList<IList<int>> ZigzagLevelOrder(TreeNode root) {
        var result = new List<IList<int>>();
        var stack = new Stack<TreeNode>();
 
        // Add root to stack
        if (root != null) {
            stack.Push(root);
        }
 
        var leftToRight = true;
        while (stack.Count > 0) {
            var queue = new Queue<TreeNode>();
            var level = new List<int>();
 
            // Add items at the top of the stack to the current level
            for (var itemCount = stack.Count; itemCount > 0; --itemCount) {
                var current = stack.Peek();
                stack.Pop();
 
                level.Add(current.val);
                queue.Enqueue(current);
            }
 
            // Add level to result
            result.Add(level);
 
            // Go through items in the queue and add them to the stack in the proper order
            for (var itemCount = queue.Count; itemCount > 0; --itemCount) {
                var current = queue.Peek();
                queue.Dequeue();
 
                // Add children to the stack
                // Left to right or Right to left order
                if (leftToRight) {
                    if (current.left != null) {
                        stack.Push(current.left);
                    }
                    if (current.right != null) {
                        stack.Push(current.right);
                    }
                } else {
                    if (current.right != null) {
                        stack.Push(current.right);
                    }
                    if (current.left != null) {
                        stack.Push(current.left);
                    }
                }
            }
            // Alternate order for the next level
            leftToRight = !leftToRight;
        }
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[[3],[20,9],[15,7]] [[1]] []

C# || How To Find Longest Duplicate Substring Using C#

October 30, 2021 admin No comments

The following is a module with functions which demonstrates how to find the longest duplicate substring using C#.

1. Longest Dup Substring – Problem Statement

Given a string s, consider all duplicated substrings: (contiguous) substrings of s that occur 2 or more times. The occurrences may overlap.

Return any duplicated substring that has the longest possible length. If s does not have a duplicated substring, the answer is “”.

Example 1:

Input: s = "banana" Output: "ana"

Example 2:

Input: s = "abcd" Output: ""

2. Longest Dup Substring – Solution

The following is a solution which demonstrates how find the longest duplicate substring.

This solution uses Binary Search and Rolling Hash.





		
		
			2. Longest Dup Substring - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the longest duplicate substring
// ============================================================================
public class Solution {
    public string LongestDupSubstring(string s) {
        // Convert string to array of ascii integers
        // to implement constant time slice
        var nums = new int[s.Length];
        for (int index = 0; index < s.Length; ++index) {
            nums[index] = (int)s[index] - (int)'a';
        }

        // Keeps track of substring start index and length
        var startIndex = -1;
        var substrLength = -1;

        // Use binary search to find the largest possible length of a duplicate substring
        var left = 1;
        var right = s.Length;
        while (left < right) {
            var mid = left + (right - left) / 2;

            // Rolling hash (Rabin-Karp)
            var index = RollingSearch(nums, mid);

            // Substring found
            if (index != -1) {
                if (mid > substrLength) {
                    startIndex = index;
                    substrLength = mid;
                }
                left = mid + 1;

            // Substring not found
            } else {
               right = mid;
            }
        }
        return substrLength != -1 ? s.Substring(startIndex, substrLength): "";
    }

    private int RollingSearch(int[] nums, int mid) {
        var seen = new HashSet<long>();

        // Base value for the rolling hash function
        var a = 31;

        // Current hash
        var hash = Hash(nums, mid, a);

        seen.Add(hash);

        long pow = 1;
        for (var index = 1; index < mid; ++index) {
            pow *= a;
        }

        var result = -1;
        for (var index = 1; index < nums.Length - mid + 1; ++index) {
            // Compute rolling hash
            hash = RollingHash(pow, hash, nums[index - 1], nums[index + mid - 1], a);

            // Hash found
            if (seen.Contains(hash)) {
                result = index;
                break;
            }
            // Hash not found
            seen.Add(hash);
        }
        return result;
    }

    private long Hash(int[] nums, int mid, int a) {
        long h = 0;
        long aL = 1;
        for (var index = mid; index >= 1; --index) {
            h += (nums[index - 1] + 1) * aL;
            aL *= a;
        }
        return h;
    }

    private long RollingHash(long pow, long hash, int left, int right, int a) {
        return (hash - (left + 1) * pow) * a + (right + 1);
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the longest duplicate substring
// ============================================================================
public class Solution {
    public string LongestDupSubstring(string s) {
        // Convert string to array of ascii integers
        // to implement constant time slice
        var nums = new int[s.Length];
        for (int index = 0; index < s.Length; ++index) {
            nums[index] = (int)s[index] - (int)'a';
        }
 
        // Keeps track of substring start index and length
        var startIndex = -1;
        var substrLength = -1;
 
        // Use binary search to find the largest possible length of a duplicate substring
        var left = 1;
        var right = s.Length;
        while (left < right) {
            var mid = left + (right - left) / 2;
 
            // Rolling hash (Rabin-Karp)
            var index = RollingSearch(nums, mid);
 
            // Substring found
            if (index != -1) {
                if (mid > substrLength) {
                    startIndex = index;
                    substrLength = mid;
                }
                left = mid + 1;
 
            // Substring not found
            } else {
               right = mid;
            }
        }
        return substrLength != -1 ? s.Substring(startIndex, substrLength): "";
    }
 
    private int RollingSearch(int[] nums, int mid) {
        var seen = new HashSet<long>();
 
        // Base value for the rolling hash function
        var a = 31;
 
        // Current hash
        var hash = Hash(nums, mid, a);
 
        seen.Add(hash);
 
        long pow = 1;
        for (var index = 1; index < mid; ++index) {
            pow *= a;
        }
 
        var result = -1;
        for (var index = 1; index < nums.Length - mid + 1; ++index) {
            // Compute rolling hash
            hash = RollingHash(pow, hash, nums[index - 1], nums[index + mid - 1], a);
 
            // Hash found
            if (seen.Contains(hash)) {
                result = index;
                break;
            }
            // Hash not found
            seen.Add(hash);
        }
        return result;
    }
 
    private long Hash(int[] nums, int mid, int a) {
        long h = 0;
        long aL = 1;
        for (var index = mid; index >= 1; --index) {
            h += (nums[index - 1] + 1) * aL;
            aL *= a;
        }
        return h;
    }
 
    private long RollingHash(long pow, long hash, int left, int right, int a) {
        return (hash - (left + 1) * pow) * a + (right + 1);
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

"ana" ""

C# || Group Anagrams – How To Group Array Of Anagrams Using C#

October 30, 2021 admin No comments

The following is a module with functions which demonstrates how to group an array of anagrams using C#.

1. Group Anagrams – Problem Statement

Given an array of strings strs, group the anagrams together. You can return the answer in any order.

An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.

Example 1:

Input: strs = ["eat","tea","tan","ate","nat","bat"] Output: [["bat"],["nat","tan"],["ate","eat","tea"]]

Example 2:

Input: strs = [""] Output: [[""]]

Example 3:

Input: strs = ["a"] Output: [["a"]]

2. Group Anagrams – Solution

The following is a solution which demonstrates how to group an array of anagrams.

The idea of this solution is to generate a simple hash key for each anagram.

The hash key is made up consisting of a digit, and a letter. These two values represents the character count, and the letter found in the given string.

For example, given the input ["eat","tea","tan","ate","nat","bat"] we create a hash for each anagram as follows:

anagram: eat, hash: 1a1e1t anagram: tea, hash: 1a1e1t anagram: tan, hash: 1a1n1t anagram: ate, hash: 1a1e1t anagram: nat, hash: 1a1n1t anagram: bat, hash: 1a1b1t

The hash key is generated similar to the counting sort technique. We use this hash to group the anagrams together.





		
		
			2. Group Anagrams - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to group anagrams
// ============================================================================
public class Solution {
    public IList<IList<string>> GroupAnagrams(string[] strs) {
        var result = new List<IList<string>>();
        var seen = new Dictionary<string, List<string>>();

        // Go through the anagrams
        foreach (var anagram in strs) {
            // Create a hash for this anagram
            var hash = Hash(anagram);

            // Check if this hash key exists
            if (!seen.ContainsKey(hash)) {
                seen[hash] = new List<string>();
            }

            // Add anagram to matching bucket
            seen[hash].Add(anagram);
        }

        // Build result
        foreach (var pair in seen) {
            result.Add(pair.Value);
        }

        return result;
    }

    private string Hash(string input) {
        var alphabet = new int[26];
        foreach (var ch in input) {
            ++alphabet[ch - 'a'];
        }
        var sb = new StringBuilder();
        for (int position = 0; position < alphabet.Length; ++position) {
            if (alphabet[position] > 0) {
                sb.Append(alphabet[position]);
                sb.Append((char)('a' + position));
            }
        }
        return sb.ToString();
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 30, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to group anagrams
// ============================================================================
public class Solution {
    public IList<IList<string>> GroupAnagrams(string[] strs) {
        var result = new List<IList<string>>();
        var seen = new Dictionary<string, List<string>>();
 
        // Go through the anagrams
        foreach (var anagram in strs) {
            // Create a hash for this anagram
            var hash = Hash(anagram);
 
            // Check if this hash key exists
            if (!seen.ContainsKey(hash)) {
                seen[hash] = new List<string>();
            }
 
            // Add anagram to matching bucket
            seen[hash].Add(anagram);
        }
 
        // Build result
        foreach (var pair in seen) {
            result.Add(pair.Value);
        }
 
        return result;
    }
 
    private string Hash(string input) {
        var alphabet = new int[26];
        foreach (var ch in input) {
            ++alphabet[ch - 'a'];
        }
        var sb = new StringBuilder();
        for (int position = 0; position < alphabet.Length; ++position) {
            if (alphabet[position] > 0) {
                sb.Append(alphabet[position]);
                sb.Append((char)('a' + position));
            }
        }
        return sb.ToString();
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[["eat","tea","ate"],["tan","nat"],["bat"]] [[""]] [["a"]]

C# || How To Traverse Binary Tree Level Order Using C#

October 29, 2021 admin No comments

The following is a module with functions which demonstrates how to traverse binary tree level order using C#.

1. Level Order – Problem Statement

Given the root of a binary tree, return the level order traversal of its nodes’ values. (i.e., from left to right, level by level).

Example 1:

Input: root = [3,9,20,null,null,15,7] Output: [[3],[9,20],[15,7]]

Example 2:

Input: root = [1] Output: [[1]]

Example 3:

Input: root = [] Output: []

2. Level Order – Solution

The following is a solution which demonstrates how to traverse binary tree level order.

This solution uses Breadth First Search to explore items at each level.





		
		
			2. Level Order - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 29, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Determines how to traverse a tree level order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public IList<IList<int>> LevelOrder(TreeNode root) {
        var result = new List<IList<int>>();
        var queue = new Queue<TreeNode>();

        if (root != null) {
            queue.Enqueue(root);
        }

        while (queue.Count > 0) {
            var level = new List<int>();

            // Loop through items in the queue
            for (var itemCount = queue.Count; itemCount > 0; --itemCount) {
                var current = queue.Peek();
                queue.Dequeue();

                // Add children to the queue if they exist
                if (current.left != null) {
                    queue.Enqueue(current.left);
                }
                if (current.right != null) {
                    queue.Enqueue(current.right);
                }

                // Add current value to the level
                level.Add(current.val);
            }

            // Add items on this level to the result
            result.Add(level);
        }

        return result;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Oct 29, 2021
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Determines how to traverse a tree level order
// ============================================================================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public IList<IList<int>> LevelOrder(TreeNode root) {
        var result = new List<IList<int>>();
        var queue = new Queue<TreeNode>();
 
        if (root != null) {
            queue.Enqueue(root);
        }
 
        while (queue.Count > 0) {
            var level = new List<int>();
 
            // Loop through items in the queue
            for (var itemCount = queue.Count; itemCount > 0; --itemCount) {
                var current = queue.Peek();
                queue.Dequeue();
 
                // Add children to the queue if they exist
                if (current.left != null) {
                    queue.Enqueue(current.left);
                }
                if (current.right != null) {
                    queue.Enqueue(current.right);
                }
 
                // Add current value to the level
                level.Add(current.val);
            }
 
            // Add items on this level to the result
            result.Add(level);
        }
 
        return result;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[[3],[9,20],[15,7]] [[1]] []

Tag Archives: leetcode

C# || How To Find The Largest Divisible Subset In Array Using C#

C# || Online Stock Span – How To Get Daily Price Stock Quotes & Consecutive Day Span Using C#

C# || How To Find Number Of Valid Words For Each Puzzle Using C#

C# || How To Implement Trie Prefix Tree Using C#

C# || How To Find Friends Of Appropriate Ages Using C#

C# || How To Get Total Sum Of Left Leaves In Binary Tree Using C#

C# || How To Get Total Sum Root To Leaf Numbers In Binary Tree Using C#

C# || Unique Paths III – How To Get The Number Of Paths From Start To End In Grid Matrix Using C#

C# || How To Capture All Surrounded Regions ‘X’ & ‘O’ In Board Matrix Using C#

C# || How To Flatten A Multilevel Doubly Linked List Using C#

C# || How To Traverse Binary Tree Zigzag Level Order Using C#

C# || How To Find Longest Duplicate Substring Using C#

C# || Group Anagrams – How To Group Array Of Anagrams Using C#

C# || How To Traverse Binary Tree Level Order Using C#

Search

Compile Your Code Now

Translate Page

Popular Pages

Recent

Archives

Categories