priority queue – My Programming Notes

Tag Archives: priority queue

C# || How To Find The Cheapest Flights Within K Stops Using C#

April 01, 2023 admin No comments

The following is a module with functions which demonstrates how to find the cheapest flights within K stops using C#.

1. Find Cheapest Price – Problem Statement

There are n cities connected by some number of flights. You are given an array flights where flights[i] = [from_i, to_i, price_i] indicates that there is a flight from city from_i to city to_i with cost price_i.

You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.

Example 1:

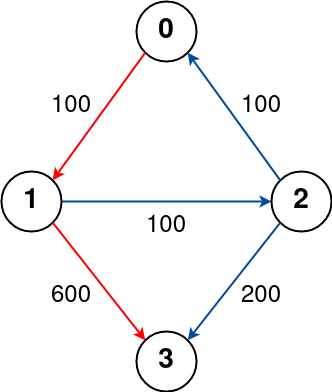
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1 Output: 700 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.

Example 2:

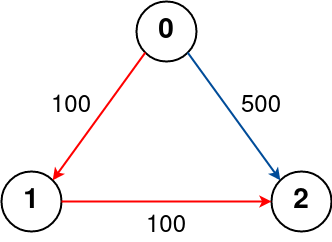
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.

Example 3:

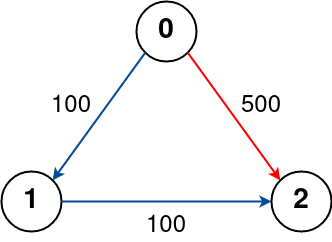
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown above. The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.

2. Find Cheapest Price – Solution

The following is a solution which demonstrates how to find the cheapest flights within K stops.





		
		
			2. Find Cheapest Price - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Apr 1, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find cheapest flights in k stops
// ============================================================================
public class Solution {
    public int FindCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        var adj = new Dictionary<int, List<int[]>>();
        foreach (int[] i in flights) {
            if (!adj.ContainsKey(i[0])) {
                adj[i[0]] = new List<int[]>();
            }
            adj[i[0]].Add(new int[] { i[1], i[2] });
        }

        int[] stops = new int[n];
        Array.Fill(stops, int.MaxValue);
        var pq = new PriorityQueue<int[], int[]>(Comparer<int[]>.Create((a, b) => a[0] - b[0]));

        // {dist_from_src_node, node, number_of_stops_from_src_node}
        var distance = new int[] { 0, src, 0 };
        pq.Enqueue(distance, distance);

        while (pq.Count > 0) {
            int[] temp = pq.Dequeue();
            int dist = temp[0];
            int node = temp[1];
            int steps = temp[2];
            // We have already encountered a path with a lower cost and fewer stops,
            // or the number of stops exceeds the limit.
            if (steps > stops[node] || steps > k + 1) {
                continue;
            }
            stops[node] = steps;
            if (node == dst) {
                return dist;
            }
            if (!adj.ContainsKey(node)) {
                continue;
            }
            foreach (int[] a in adj[node]) {
                var newDistance = new int[] { dist + a[1], a[0], steps + 1 };
                pq.Enqueue(newDistance, newDistance);
            }
        }
        return -1;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Apr 1, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find cheapest flights in k stops
// ============================================================================
public class Solution {
    public int FindCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        var adj = new Dictionary<int, List<int[]>>();
        foreach (int[] i in flights) {
            if (!adj.ContainsKey(i[0])) {
                adj[i[0]] = new List<int[]>();
            }
            adj[i[0]].Add(new int[] { i[1], i[2] });
        }
 
        int[] stops = new int[n];
        Array.Fill(stops, int.MaxValue);
        var pq = new PriorityQueue<int[], int[]>(Comparer<int[]>.Create((a, b) => a[0] - b[0]));
 
        // {dist_from_src_node, node, number_of_stops_from_src_node}
        var distance = new int[] { 0, src, 0 };
        pq.Enqueue(distance, distance);
 
        while (pq.Count > 0) {
            int[] temp = pq.Dequeue();
            int dist = temp[0];
            int node = temp[1];
            int steps = temp[2];
            // We have already encountered a path with a lower cost and fewer stops,
            // or the number of stops exceeds the limit.
            if (steps > stops[node] || steps > k + 1) {
                continue;
            }
            stops[node] = steps;
            if (node == dst) {
                return dist;
            }
            if (!adj.ContainsKey(node)) {
                continue;
            }
            foreach (int[] a in adj[node]) {
                var newDistance = new int[] { dist + a[1], a[0], steps + 1 };
                pq.Enqueue(newDistance, newDistance);
            }
        }
        return -1;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

700 200 500

C# || How To Remove Stones To Minimize The Total Using C#

February 01, 2023 admin No comments

The following is a module with functions which demonstrates how to remove stones to minimize the total using C#.

1. Min Stone Sum – Problem Statement

You are given a 0-indexed integer array piles, where piles[i] represents the number of stones in the i^th pile, and an integer k. You should apply the following operation exactly k times:

Choose any piles[i] and remove floor(piles[i] / 2) stones from it.

Notice that you can apply the operation on the same pile more than once.

Return the minimum possible total number of stones remaining after applying the k operations.

floor(x) is the greatest integer that is smaller than or equal to x (i.e., rounds x down).

Example 1:

Input: piles = [5,4,9], k = 2 Output: 12 Explanation: Steps of a possible scenario are: - Apply the operation on pile 2. The resulting piles are [5,4,5]. - Apply the operation on pile 0. The resulting piles are [3,4,5]. The total number of stones in [3,4,5] is 12.

Example 2:

Input: piles = [4,3,6,7], k = 3 Output: 12 Explanation: Steps of a possible scenario are: - Apply the operation on pile 2. The resulting piles are [4,3,3,7]. - Apply the operation on pile 3. The resulting piles are [4,3,3,4]. - Apply the operation on pile 0. The resulting piles are [2,3,3,4]. The total number of stones in [2,3,3,4] is 12.

2. Min Stone Sum – Solution

The following is a solution which demonstrates how to remove stones to minimize the total.





		
		
			2. Min Stone Sum - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Feb 1, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to remove stones to minimize the total
// ============================================================================
public class Solution {
    public int MinStoneSum(int[] piles, int k) {
        var heap = new PriorityQueue<int, int>(Comparer<int>.Create((a, b) => b - a));
        int totalSum = 0;

        foreach (int num in piles) {
            heap.Enqueue(num, num);
            totalSum += num;
        }

        for (int index = 0; index < k; ++index) {
            int currentValue = heap.Dequeue();
            int removeFromTotal = currentValue / 2;
            int newValue = currentValue - removeFromTotal;
            heap.Enqueue(newValue, newValue);
            totalSum -= removeFromTotal;
        }

        return totalSum;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Feb 1, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to remove stones to minimize the total
// ============================================================================
public class Solution {
    public int MinStoneSum(int[] piles, int k) {
        var heap = new PriorityQueue<int, int>(Comparer<int>.Create((a, b) => b - a));
        int totalSum = 0;
 
        foreach (int num in piles) {
            heap.Enqueue(num, num);
            totalSum += num;
        }
 
        for (int index = 0; index < k; ++index) {
            int currentValue = heap.Dequeue();
            int removeFromTotal = currentValue / 2;
            int newValue = currentValue - removeFromTotal;
            heap.Enqueue(newValue, newValue);
            totalSum -= removeFromTotal;
        }
 
        return totalSum;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

12 12

C# || Single-Threaded CPU – How To Find The Order CPU Will Process Tasks Using C#

January 27, 2023 admin No comments

The following is a module with functions which demonstrates how to find the order CPU will process tasks using C#.

1. Get Order – Problem Statement

You are given n tasks labeled from 0 to n – 1 represented by a 2D integer array tasks, where tasks[i] = [enqueueTime_i, processingTime_i] means that the i^th task will be available to process at enqueueTime_i and will take processingTime_ito finish processing.

You have a single-threaded CPU that can process at most one task at a time and will act in the following way:

If the CPU is idle and there are no available tasks to process, the CPU remains idle.
If the CPU is idle and there are available tasks, the CPU will choose the one with the shortest processing time. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
Once a task is started, the CPU will process the entire task without stopping.
The CPU can finish a task then start a new one instantly.

Return the order in which the CPU will process the tasks.

Example 1:

Input: tasks = [[1,2],[2,4],[3,2],[4,1]] Output: [0,2,3,1] Explanation: The events go as follows: - At time = 1, task 0 is available to process. Available tasks = {0}. - Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}. - At time = 2, task 1 is available to process. Available tasks = {1}. - At time = 3, task 2 is available to process. Available tasks = {1, 2}. - Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}. - At time = 4, task 3 is available to process. Available tasks = {1, 3}. - At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}. - At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}. - At time = 10, the CPU finishes task 1 and becomes idle.

Example 2:

Input: tasks = [[7,10],[7,12],[7,5],[7,4],[7,2]] Output: [4,3,2,0,1] Explanation: The events go as follows: - At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}. - Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}. - At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}. - At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}. - At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}. - At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}. - At time = 40, the CPU finishes task 1 and becomes idle.

2. Get Order – Solution

The following is a solution which demonstrates how to find the order CPU will process tasks.





		
		
			2. Get Order - Solution
			
C#
			
			// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jan 27, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the order CPU will process tasks
// ============================================================================
public class Solution {
    private const int ENQUEUE_TIME = 0;
    private const int PROCESSING_TIME = 1;
    private const int INDEX = 2;

    public int[] GetOrder(int[][] tasks) {
        // Sort based on min task processing time or min task index.
        // Store enqueue time, processing time, task index.
        var nextTask = new PriorityQueue<int[], int[]>(Comparer<int[]>.Create((a, b) => (a[PROCESSING_TIME] != b[PROCESSING_TIME] ? (a[PROCESSING_TIME] - b[PROCESSING_TIME]) : (a[INDEX] - b[INDEX]))));

        // Store task enqueue time, processing time, index.
        int[][] sortedTasks = new int[tasks.Length][];
        for (int index = 0; index < sortedTasks.Length; ++index) {
            sortedTasks[index] = new int[3];
        }
        for (int index = 0; index < tasks.Length; ++index) {
            sortedTasks[index][ENQUEUE_TIME] = tasks[index][ENQUEUE_TIME];
            sortedTasks[index][PROCESSING_TIME] = tasks[index][PROCESSING_TIME];
            sortedTasks[index][INDEX] = index;
        }

        Array.Sort(sortedTasks, (a, b) => a[ENQUEUE_TIME] - b[ENQUEUE_TIME]);
        int[] tasksProcessingOrder = new int[tasks.Length];

        long currentTime = 0;
        int taskIndex = 0;
        int ansIndex = 0;

        // Stop when no tasks are left in array and heap.
        while (taskIndex < tasks.Length || nextTask.Count > 0) {
            if (nextTask.Count == 0 && currentTime < sortedTasks[taskIndex][ENQUEUE_TIME]) {
                // When the heap is empty, try updating currentTime to next task's enqueue time.
                currentTime = sortedTasks[taskIndex][ENQUEUE_TIME];
            }

            // Push all the tasks whose enqueueTime <= currtTime into the heap.
            while (taskIndex < tasks.Length && currentTime >= sortedTasks[taskIndex][ENQUEUE_TIME]) {
                nextTask.Enqueue(sortedTasks[taskIndex], sortedTasks[taskIndex]);
                ++taskIndex;
            }

            int[] task = nextTask.Dequeue();
            int processTime = task[PROCESSING_TIME];
            int index = task[INDEX];

            // Complete this task and increment currentTime.
            currentTime += processTime;
            tasksProcessingOrder[ansIndex++] = index;
        }

        return tasksProcessingOrder;
    }
}// http://programmingnotes.org/
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
				
						// ============================================================================
//    Author: Kenneth Perkins
//    Date:   Jan 27, 2023
//    Taken From: http://programmingnotes.org/
//    File:  Solution.cs
//    Description: Demonstrates how to find the order CPU will process tasks
// ============================================================================
public class Solution {
    private const int ENQUEUE_TIME = 0;
    private const int PROCESSING_TIME = 1;
    private const int INDEX = 2;
 
    public int[] GetOrder(int[][] tasks) {
        // Sort based on min task processing time or min task index.
        // Store enqueue time, processing time, task index.
        var nextTask = new PriorityQueue<int[], int[]>(Comparer<int[]>.Create((a, b) => (a[PROCESSING_TIME] != b[PROCESSING_TIME] ? (a[PROCESSING_TIME] - b[PROCESSING_TIME]) : (a[INDEX] - b[INDEX]))));
 
        // Store task enqueue time, processing time, index.
        int[][] sortedTasks = new int[tasks.Length][];
        for (int index = 0; index < sortedTasks.Length; ++index) {
            sortedTasks[index] = new int[3];
        }
        for (int index = 0; index < tasks.Length; ++index) {
            sortedTasks[index][ENQUEUE_TIME] = tasks[index][ENQUEUE_TIME];
            sortedTasks[index][PROCESSING_TIME] = tasks[index][PROCESSING_TIME];
            sortedTasks[index][INDEX] = index;
        }
 
        Array.Sort(sortedTasks, (a, b) => a[ENQUEUE_TIME] - b[ENQUEUE_TIME]);
        int[] tasksProcessingOrder = new int[tasks.Length];
 
        long currentTime = 0;
        int taskIndex = 0;
        int ansIndex = 0;
 
        // Stop when no tasks are left in array and heap.
        while (taskIndex < tasks.Length || nextTask.Count > 0) {
            if (nextTask.Count == 0 && currentTime < sortedTasks[taskIndex][ENQUEUE_TIME]) {
                // When the heap is empty, try updating currentTime to next task's enqueue time.
                currentTime = sortedTasks[taskIndex][ENQUEUE_TIME];
            }
 
            // Push all the tasks whose enqueueTime <= currtTime into the heap.
            while (taskIndex < tasks.Length && currentTime >= sortedTasks[taskIndex][ENQUEUE_TIME]) {
                nextTask.Enqueue(sortedTasks[taskIndex], sortedTasks[taskIndex]);
                ++taskIndex;
            }
 
            int[] task = nextTask.Dequeue();
            int processTime = task[PROCESSING_TIME];
            int index = task[INDEX];
 
            // Complete this task and increment currentTime.
            currentTime += processTime;
            tasksProcessingOrder[ansIndex++] = index;
        }
 
        return tasksProcessingOrder;
    }
}// http://programmingnotes.org/

QUICK NOTES:
The highlighted lines are sections of interest to look out for.

The code is heavily commented, so no further insight is necessary. If you have any questions, feel free to leave a comment below.

Once compiled, you should get this as your output for the example cases:

[0,2,3,1] [4,3,2,0,1]

Tag Archives: priority queue

C# || How To Find The Cheapest Flights Within K Stops Using C#

C# || How To Remove Stones To Minimize The Total Using C#

C# || Single-Threaded CPU – How To Find The Order CPU Will Process Tasks Using C#

Search

Compile Your Code Now

Translate Page

Popular Pages

Recent

Archives

Categories